A fizikai kémia kissé tág témakör; a következő témaköröket öleli fel:

• Kvantumkémia
• Thermokémia (áttekintés + több)
• Kinetika (áttekintés + több)
• Statisztikai mechanika

Mivel elég sok téma van egy válaszhoz, ezért témánként csak két példát adok. Ez egy hosszú válasz lesz, de koncentrálhatsz arra, amit keresel.

KVANTUMKÉMIA

A kvantumkémia általában arról szól, hogy megpróbáljuk megérteni a pikoszkopikus léptékű forgatókönyveket, a rendszereket kényelmes matematikai ábrázolásokban modellezni és a megfelelő közelítéseket elvégezni.

A kvantumkémia két példája a következő:

• Egyszerű harmonikus oszcillátor (két golyó, amelyeket ideális rugó köt össze)

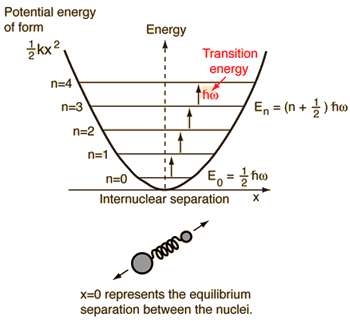
Ezt a rendszert, amelyet a fizikából ismerünk, kéttestű klasszikus problémából egytestű problémára redukáljuk relatív koordinátákkal és csökkentett tömeggel, #mu = (m_1m_2)/(m_1 + m_2)#.

Ez a rendszer a molekuláris kötés rugalmas potenciális energiájának megértésére összpontosít.

• Merev rotor (két golyó egy rúddal összekötve, azaz 100%-os merev rugó)

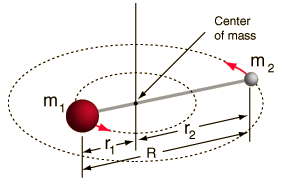
Ez a rendszer egy egyszerűsítés, mivel minden molekulában van valamilyen kötésnyújtás/rezgés (ha látnád a matematikát, megértenéd, miért jó ez az egyszerűsítés!).

Mégis lehetővé teszi számunkra, hogy egy kéttestes rendszer e szögkomponensét felbontjuk, és megértsük a molekula forgási tulajdonságait.

THERMOKÉMIA

Ez a hőáramlás, a munka, a szabad energiák stb. makroszkopikus léptékét vizsgálja. Ezt már az általános kémiában valamennyire megtetted, és ezt ismétli és bővíti.

Két példa:

• Thermodinamikai értékek meghatározása mérhető mennyiségekből

Mi a kémia, ha nem gyakorlatias?

A közös téma tehát az, hogy képesek legyünk levezetéseket végezni és a főbb termodinamikai mennyiségeket (entrópia, entalpia, gibbs + helmholtz szabad energia, belső energia) természetes változókkal, például térfogattal, hőmérséklettel és nyomással kifejezni.

Például izotermikus tágulásból (#DeltaT = 0, DeltaV > 0#) kiszámíthatjuk az entrópiát, ha ismerjük a #V_2# és a #V_1#, vagy a #P_2# és a #P_1# értékeket, mégpedig egy egyatomos ideális gázra:

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Ideális és nem ideális nem-elektrolit/elektrolit oldatok

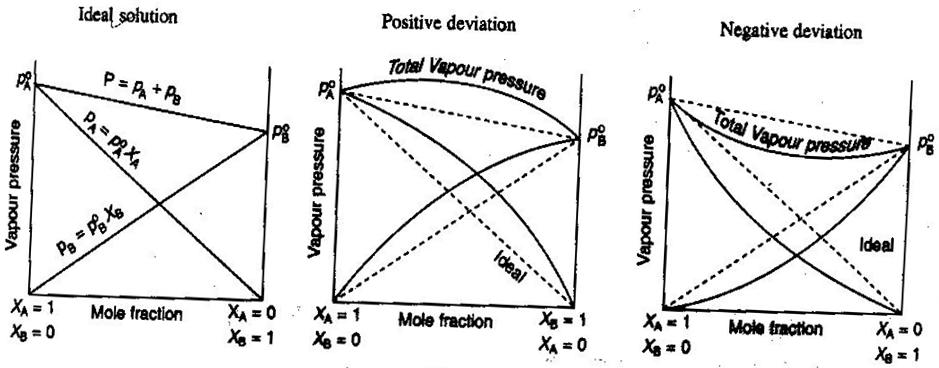
Az általános kémiában, szeretjük az oldatokat ideálisan kezelni, így a térfogatok additívek, az erős elektrolitok koncentrációi egyenes #”mol/L “# számítások, és így tovább. Néhány módja annak, hogy az oldatok nem ideálisak:

• Az oldat keverés után tágulhat vagy összehúzódhat.
• A ionpárosítás csökkenti az oldat ionerősségét és csökkenti az oldott anyag #i# van’t Hoff-tényezőjét.
• Az oldott anyag szökési hajlama megváltoztatja az effektív koncentrációját (aktivitását).

KINETIKA

Ezzel talán már foglalkoztál általános kémiaórán, vagy esetleg középiskolában. A fizikai kémia ezt egy kicsit jobban kibővíti a reakciómechanizmusok és a gázfázis dinamikájának részletesebb vizsgálatával.

Két példa:

• állandósult állapot közelítése

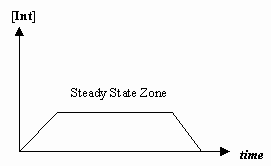
Néha az első mechanikai lépés sebessége sokkal lassabb, mint a második lépésé, és úgy közelítünk, hogy a köztes termék koncentrációja ténylegesen nem változik (#(d)/(dt) = 0#).

Ez lehetővé teszi egy mechanizmusra jellemző sebességtörvény levezetését, és azt, hogy az egyes lépések sebességállandói alapján kifejezzünk egy “megfigyelt sebességállandót”.

• Reális gáztörvények

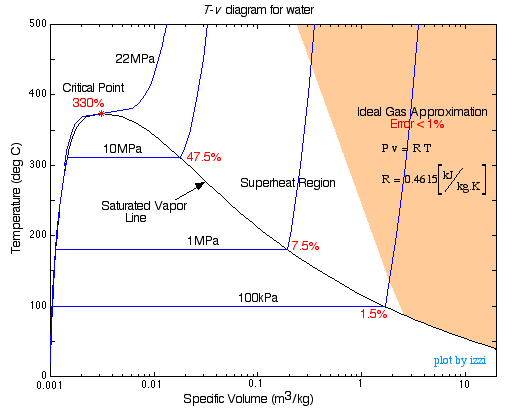
A van der Waals-állapotegyenletet már megismerhettétek:

#(V – nb) = nRT#

Nos, van még néhány, például a Redlich-Kwong, a Peng-Robinson és így tovább.

Az alapgondolat az, hogy ezek mind jobban működnek bizonyos gázok esetében, mint mások, de mind a gázok valós tulajdonságainak figyelembevételével működnek, ahelyett, hogy azt feltételeznénk, hogy mindenki egy rugalmasan ütköző, inert ponttömeg.

STATISZTIKAI MECHANIKA

A statisztikai mechanikával egy lépést hátrálunk, és a pikoszkopikus világot makroszkopikus szemszögből vizsgáljuk:

“Mit tudhatunk meg egy rendszerről, ha kvantumkémikusként gondolkodunk egy nagy részecskegyűjteményről?”

Két példa:

• Equipartíciós tétel

#<< K >> = N/2nRT = N/2 k_BT#,

ahol #N# az egyes mozgástípusok (lineáris, rotációs, rezgési, elektronikus, nukleáris) szabadságfokainak száma. Alapvetően a molekula minden mozgástípusát figyelembe veszi, hogy megbecsülje annak átlagos mozgási energiáját, #<< K >>#.

Ez csak “elég magas” hőmérsékleten működik. Általában a transzlációs és rotációs mozgások esetében rendben van, de hajlamos túlbecsülni a rezgési hozzájárulásokat.

• A mikrokanonikus eloszlásfüggvény

#q = sum_(i=1)^(N) g_ie^(-béta epsilon_i)#,

hol:

• #g_i# az #i# állapot elfajulása #epsilon_i# energiával.
• #N# a rendelkezésre álló állapotok teljes száma.

Mint ahogy a #psi# hullámfüggvény mindent megad, amit egy kvantummechanikai rendszerről tudni lehet, úgy a mikrokanonikus partíciós függvény azt adja meg, hogy egy molekula hogyan oszthatja el a rendelkezésre álló energiáját a lehetséges állapottípusok (transzlációs, rotációs, rezgési, elektronikus és nukleáris) között.

Minden állapottípushoz létezik egy #q#: #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)# és #q_(n uc)#.

Az egyes #q# típusok ismeretében az egyes #q# típusokra vonatkoztatva levezethetők az ismert termodinamikai mennyiségek, mint például az entrópia (#S#), az entalpia (#H#), a Gibbs-féle szabad energia (#G#) stb.

Az abszolút molekuláris entrópia MINDEN hőmérsékleten a legtöbb esetben a következőképpen számítható ki:

#S/N = k_B ln (q/N)_”tot” + (<< epsilon >>_”tot”)/T + k_B#,

hol:

• #k_B ~~”0.695 cm”^(-1)”/K “# a Boltzmann-állandó.
• #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# a teljes mikrokanonikus partíciós függvény, amely az összes lehetséges állapottípust tartalmazza, és #N# a figyelembe vett molekulák teljes száma.
• #<< epsilon >> = E/N# a molekuláris energia, amelyet a következőképpen határozunk meg: #<< epsilon >> = k_BT^2((del ln (q”/”N)_”tot”)/(del T))_V#.

(Igen, ez a képlet #”298,15 K “# esetén lehetővé teszi ugyanannak az #S^@#-nak a kiszámítását, mint amit a tankönyv függelékében lát!)

Egy példa erre a képletre használatban itt található.