Le strutture di dati ad albero hanno molti usi, ed è bene avere una comprensione di base del loro funzionamento. Gli alberi sono la base per altre strutture dati molto usate come le Mappe e gli Insiemi. Inoltre, sono usati nei database per eseguire ricerche veloci. Il DOM HTML usa una struttura dati ad albero per rappresentare la gerarchia degli elementi. Questo post esplorerà i diversi tipi di alberi come gli alberi binari, gli alberi di ricerca binaria, e come implementarli.

Abbiamo esplorato le strutture dati Graph nel post precedente, che sono un caso generalizzato di alberi. Cominciamo a imparare cosa sono le strutture dati ad albero!

Questo post fa parte di una serie di tutorial:

Imparare strutture dati e algoritmi (DSA) per principianti

1. Introduzione alla complessità temporale degli algoritmi e notazione Big O

2. Otto complessità temporali che ogni programmatore dovrebbe conoscere

3. Strutture dati per principianti: Array, HashMap e Liste

4. Strutture di dati grafici per principianti

5. Strutture di dati ad albero per principianti 👈 sei qui

6. Alberi di ricerca binari autobilanciati

7. Appendice I: Analisi degli algoritmi ricorsivi

Alberi: concetti di base

Un albero è una struttura dati dove un nodo può avere zero o più figli. Ogni nodo contiene un valore. Come i grafi, la connessione tra i nodi è chiamata bordi. Un albero è un tipo di grafo, ma non tutti i grafi sono alberi (ne parleremo più avanti).

Queste strutture di dati sono chiamate “alberi” perché la struttura dei dati assomiglia ad un albero 🌳. Inizia con un nodo radice e si ramifica con i suoi discendenti, e infine, ci sono le foglie.

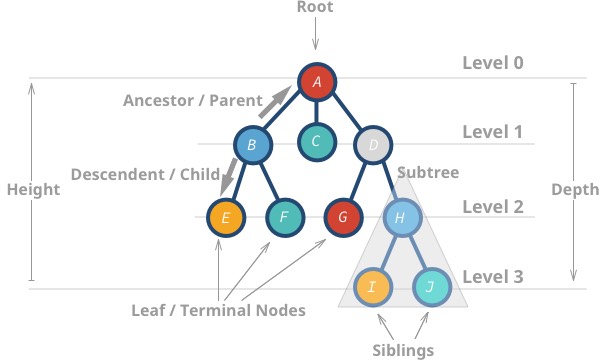
Ecco alcune proprietà degli alberi:

• Il nodo più in alto è chiamato radice.
• Un nodo senza figli è chiamato nodo foglia o nodo terminale.
• L’altezza (h) dell’albero è la distanza (conteggio dei bordi) tra la foglia più lontana e la radice.
  • A ha un’altezza di 3
  • I ha un’altezza di 0
• La profondità o livello di un nodo è la distanza tra la radice e il nodo in questione.
  • H ha una profondità di 2
  • B ha una profondità di 1

Implementare una semplice struttura dati ad albero

Come abbiamo visto prima, un nodo dell’albero è solo una struttura dati con un valore e collegamenti ai suoi discendenti.

Ecco un esempio di un nodo albero:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Possiamo creare un albero con 3 discendenti come segue:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Questo è tutto; abbiamo una struttura dati ad albero!

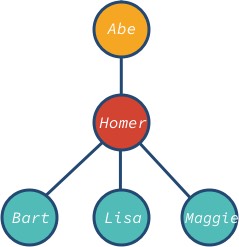
Il nodo abe è la radice e bart, lisa e maggie sono i nodi foglia dell’albero. Notate che il nodo dell’albero può avere diversi discendenti: 0, 1, 3, o qualsiasi altro valore.

Le strutture dati ad albero hanno molte applicazioni come:

• Mappe
• Insiemi
• Base di dati
• Code di priorità
• Interrogazione di un LDAP (Lightweight Directory Access Protocol)
• Rappresentazione del Document Object Model (DOM) per HTML sui siti web.

Alberi binari

I nodi degli alberi possono avere zero o più figli. Tuttavia, quando un albero ha al massimo due figli, allora si chiama albero binario.

Alberi binari completi, completi e perfetti

A seconda di come i nodi sono disposti in un albero binario, esso può essere completo, completo e perfetto:

• Albero binario completo: ogni nodo ha esattamente 0 o 2 figli (ma mai 1).
• Albero binario completo: quando tutti i livelli tranne l’ultimo sono pieni di nodi.
• Albero binario perfetto: quando tutti i livelli (compreso l’ultimo) sono pieni di nodi.

Guarda questi esempi:

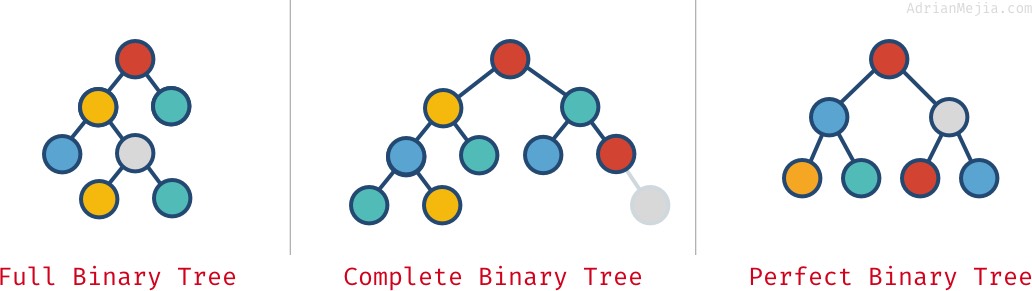
Queste proprietà non sono sempre mutualmente esclusive. Puoi averne più di una:

• Un albero perfetto è sempre completo e pieno.
  • Gli alberi binari perfetti hanno precisamente `2^k – 1` nodi, dove k è l’ultimo livello dell’albero (che inizia con 1).
• Un albero completo non è sempre full.
  • Come nel nostro esempio “completo”, poiché ha un genitore con un solo figlio. Se rimuoviamo il nodo grigio più a destra, allora avremmo un albero completo, ma non perfetto.
• Un albero completo non è sempre completo e perfetto.

Albero di ricerca binario (BST)

Gli alberi di ricerca binari o BST in breve sono una particolare applicazione degli alberi binari. BST ha al massimo due nodi (come tutti gli alberi binari). Tuttavia, i valori sono tali che il valore dei figli di sinistra deve essere minore del genitore, e i figli di destra devono essere maggiori.

Duplicati: Alcuni BST non permettono i duplicati mentre altri aggiungono gli stessi valori di un figlio di destra. Altre implementazioni potrebbero tenere un conteggio su un caso di duplicità (questo lo faremo più tardi).

Implementiamo un albero di ricerca binario!

Implementazione BST

I BST sono molto simili alla nostra precedente implementazione di un albero. Tuttavia, ci sono alcune differenze:

• I nodi possono avere, al massimo, solo due figli: sinistra e destra.
• I valori dei nodi devono essere ordinati come left < parent < right.

Ecco il nodo dell’albero. Molto simile a quello che abbiamo fatto prima, ma abbiamo aggiunto alcuni comodi getter e setter per i figli di sinistra e di destra. Notate che sta anche mantenendo un riferimento al genitore, e lo aggiorniamo ogni volta che aggiungiamo dei figli.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Ok, finora, possiamo aggiungere un figlio sinistro e destro. Ora, facciamo la classe BST che fa rispettare la regola left < parent < right.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Implementiamo l’inserimento.

Inserimento nodo BST

Per inserire un nodo in un albero binario, facciamo quanto segue:

1. Se l’albero è vuoto, il primo nodo diventa la radice, e il gioco è fatto.
2. Confronta il valore di radice/padre se è più alto vai a destra, se è più basso vai a sinistra. Se è lo stesso, allora il valore esiste già in modo da poter aumentare il conteggio dei duplicati (molteplicità).
3. Ripetere #2 fino a quando abbiamo trovato uno slot vuoto per inserire il nuovo nodo.

Facciamo un’illustrazione di come inserire 30, 40, 10, 15, 12, 50:

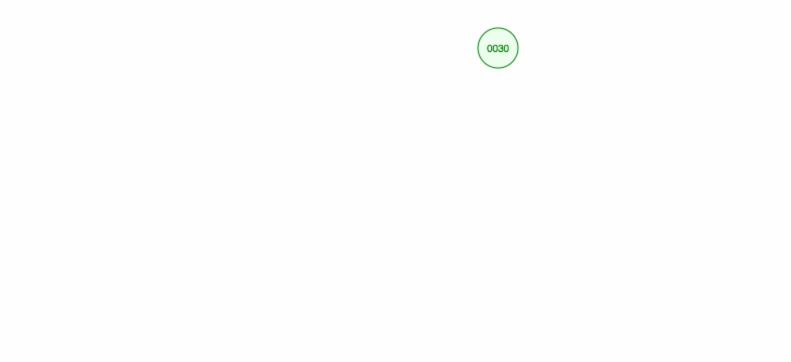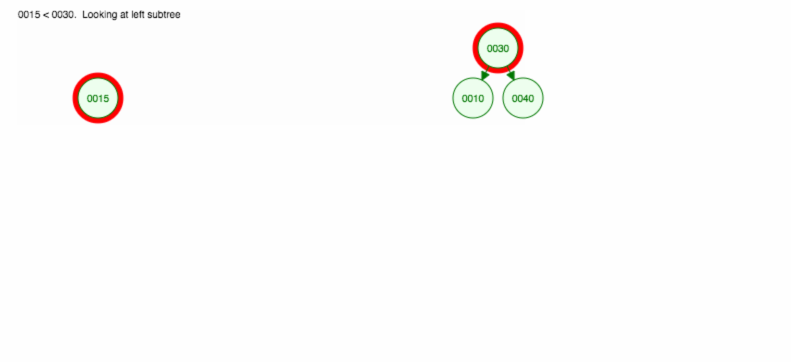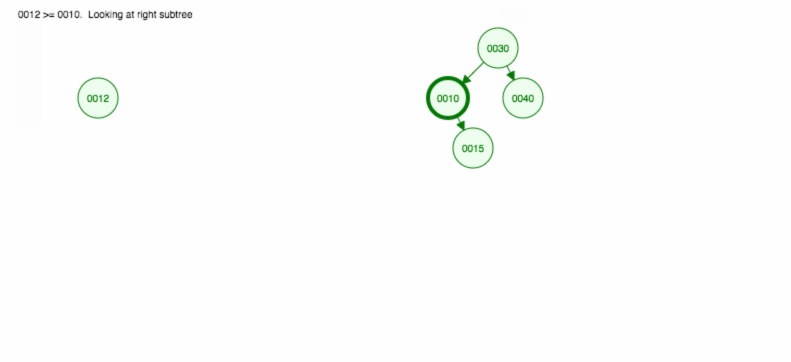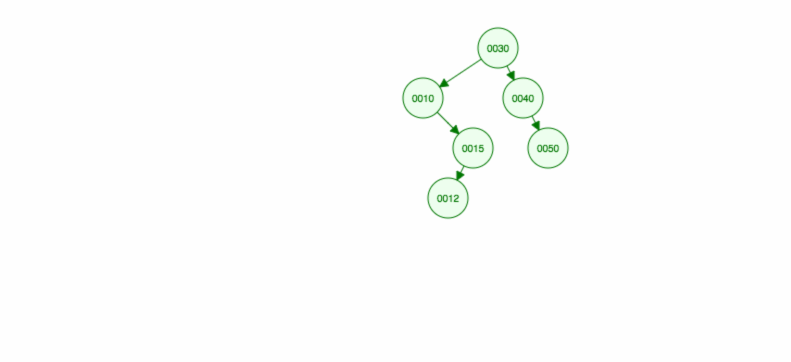
Possiamo implementare insert come segue:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Stiamo usando una funzione helper chiamata findNodeAndParent. Se abbiamo trovato che il nodo esiste già nell’albero, allora aumentiamo il contatore multiplicity. Vediamo come è implementata questa funzione:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent attraversa l’albero, cercando il valore. Inizia dalla radice (linea 2) e poi va a sinistra o a destra in base al valore (linea 10). Se il valore esiste già, restituisce il nodo found e anche il genitore. Nel caso che il nodo non esista, restituiamo ancora il nodo parent.

BST Node Deletion

Sappiamo come inserire e cercare il valore. Ora, stiamo per implementare l’operazione di cancellazione. E’ un po’ più complicata dell’aggiunta, quindi spieghiamola con i seguenti casi:

Eliminazione di un nodo foglia (0 figli)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Eliminiamo il riferimento dal genitore del nodo (15) per essere nullo.

Eliminazione di un nodo con un figlio.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

In questo caso, andiamo al genitore (30) e sostituiamo il figlio (10) con un figlio del figlio (15).

Eliminare un nodo con due figli

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Stiamo eliminando il nodo 40, che ha due figli (35 e 50). Sostituiamo il figlio (30) del genitore (40) con il figlio destro del figlio (50). Poi teniamo il figlio sinistro (35) nello stesso posto di prima, quindi dobbiamo renderlo il figlio sinistro di 50.

Un altro modo per rimuovere il nodo 40 è spostare il figlio sinistro (35) in alto e poi mantenere il figlio destro (50) dove era.

1
2
3
4
5

 30
/ \
15 35
\
50

Entrambi i modi vanno bene finché si mantiene la proprietà dell’albero di ricerca binario: left < parent < right.

Eliminare la radice.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Eliminare la radice è molto simile alla rimozione dei nodi con 0, 1, o 2 figli discussa in precedenza. L’unica differenza è che dopo, abbiamo bisogno di aggiornare il riferimento della radice dell’albero.

Ecco un’animazione di ciò che abbiamo discusso.

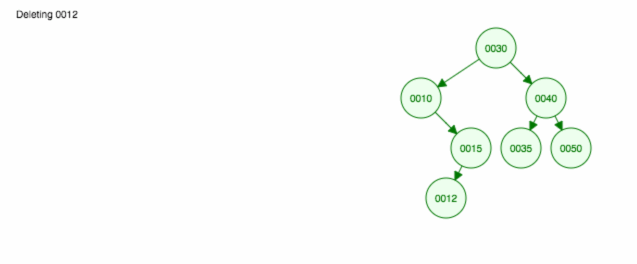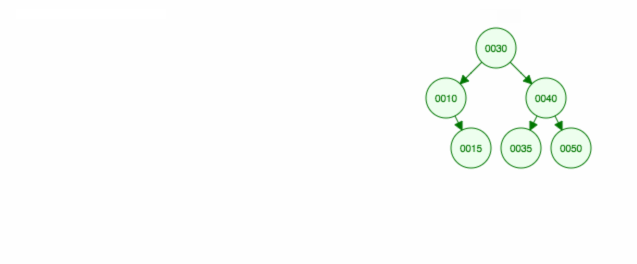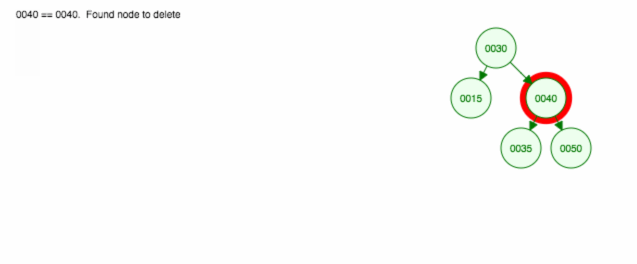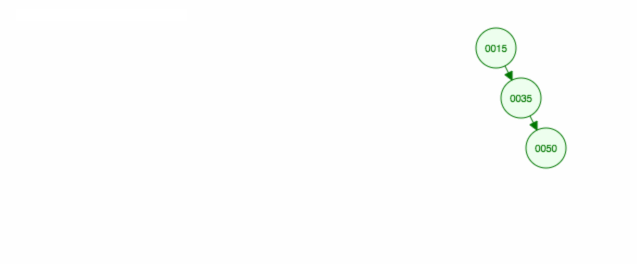
L’animazione sposta il figlio/sottoalbero di sinistra e mantiene il figlio/sottoalbero di destra al suo posto.

Ora che abbiamo una buona idea di come dovrebbe funzionare, implementiamola:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Ecco alcuni punti salienti dell’implementazione:

• Primo, cerchiamo se il nodo esiste. Se non esiste, restituiamo false, e abbiamo finito!
• Se il nodo da rimuovere esiste, allora combiniamo i figli di sinistra e di destra in un unico sottoalbero.
• Sostituiamo il nodo da eliminare con il sottoalbero combinato.

La funzione che combina il sottoalbero di sinistra in quello di destra è la seguente:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Per esempio, diciamo che vogliamo combinare il seguente albero, e stiamo per cancellare il nodo 30. Vogliamo mescolare il sottoalbero di sinistra del 30 con quello di destra. Il risultato è questo:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Se facciamo diventare il nuovo sottoalbero la radice, allora il nodo 30 non è più!

Trasversale dell’albero binario

Ci sono diversi modi di attraversare un albero binario, a seconda dell’ordine in cui i nodi sono visitati: in-order, pre-order e post-order. Inoltre, possiamo usareDFSeBFSche abbiamo imparato dal postgraph.

In-Order Traversal

In-order traversal visita i nodi in questo ordine: sinistra, genitore, destra.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Utilizziamo questo albero per fare l’esempio:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

In-order traversal stamperebbe i seguenti valori: 3, 4, 5, 10, 15, 30, 40. Se l’albero è un BST, allora i nodi saranno ordinati in ordine ascendente come nel nostro esempio.

Post-Order Traversal

Post-order traversal visita i nodi in questo ordine: left, right, parent.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversal stampa i seguenti valori: 3, 4, 5, 15, 40, 30, 10.

Pre-Order Traversal e DFS

Pre-order traversal visita i nodi in questo ordine: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversal stamperebbe i seguenti valori: 10, 5, 4, 3, 30, 15, 40. Questo ordine di numeri è lo stesso risultato che otterremmo se eseguissimo la Depth-First Search (DFS).

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Se avete bisogno di un ripasso sulla DFS, ne abbiamo parlato in dettaglio nel post Graph.

Ricerca per primi (BFS)

Simile a DFS, possiamo implementare un BFS cambiando il Stack con un Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

L’ordine BFS è: 10, 5, 30, 4, 15, 40, 3

Alberi bilanciati contro alberi non bilanciati

Finora abbiamo discusso come add, remove e find elementi. Tuttavia, non abbiamo parlato dei tempi di esecuzione. Pensiamo agli scenari peggiori.

Diciamo che vogliamo aggiungere numeri in ordine crescente.

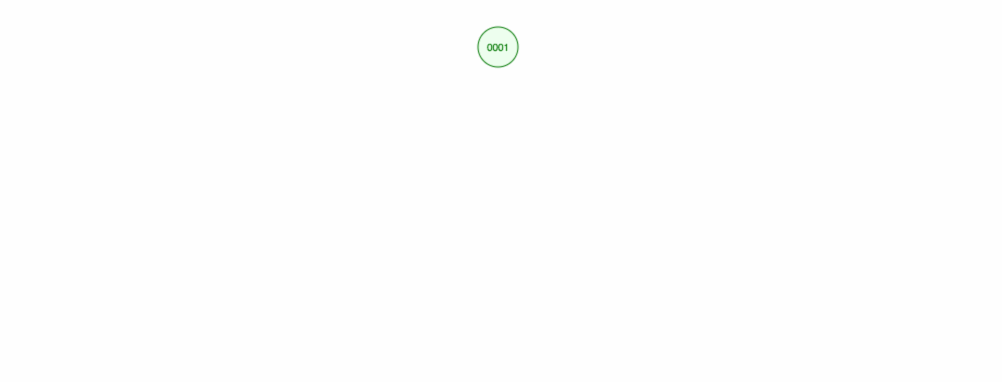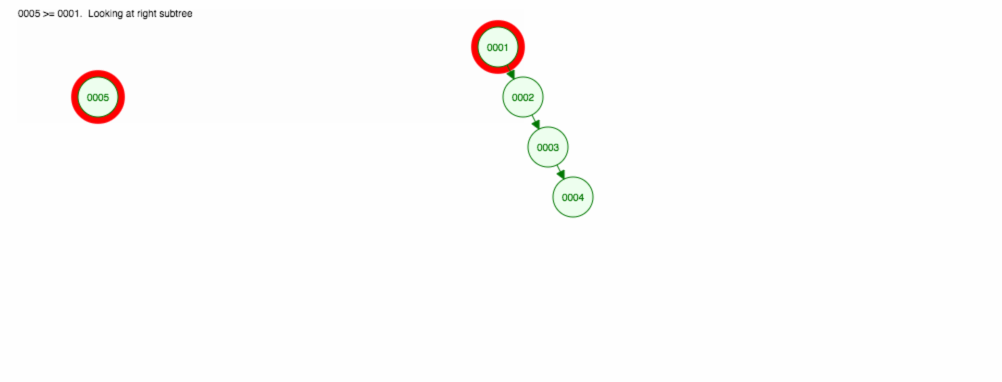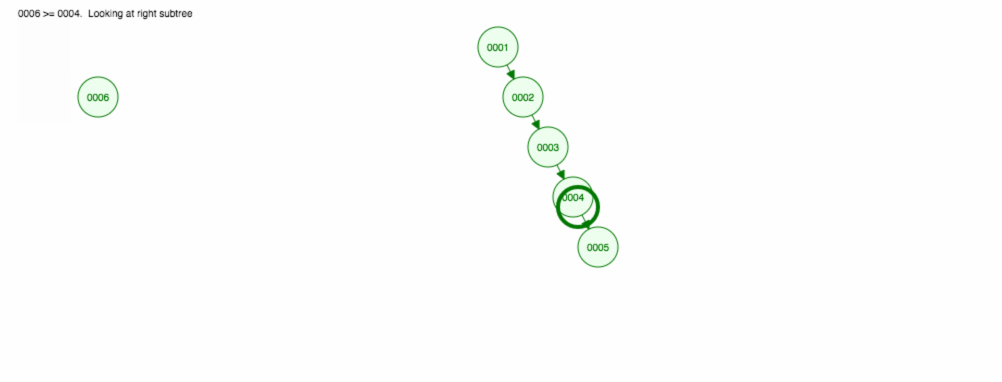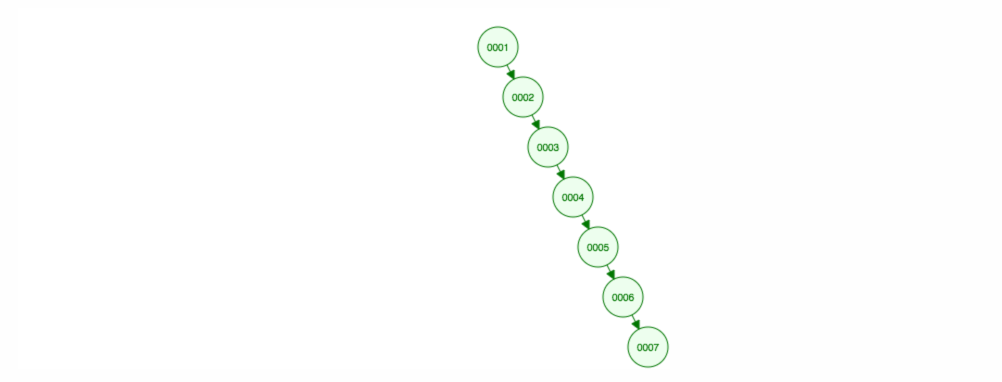
Finiamo con tutti i nodi sulla destra! Questo albero sbilanciato non è meglio di una LinkedList, quindi trovare un elemento richiederebbe O(n). 😱

Cercare qualcosa in un albero sbilanciato è come cercare una parola nel dizionario pagina per pagina. Quando l’albero è bilanciato, puoi aprire il dizionario al centro, e da lì, sai se devi andare a sinistra o a destra a seconda dell’alfabeto e della parola che stai cercando.

Dobbiamo trovare un modo per bilanciare l’albero!

Se l’albero fosse bilanciato, potremmo trovare elementi in O(log n) invece di passare attraverso ogni nodo. Parliamo di cosa significa un albero bilanciato.

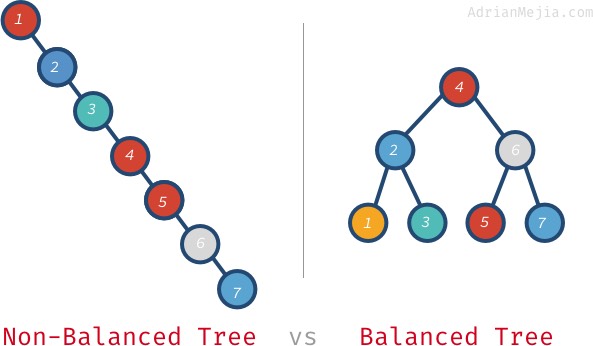
Se cerchiamo 7 nell’albero non bilanciato, dobbiamo andare da 1 a 7. Tuttavia, nell’albero bilanciato, visitiamo: 4, 6 e 7. Diventa ancora peggio con alberi più grandi. Se avete un milione di nodi, la ricerca di un elemento inesistente potrebbe richiedere la visita di tutto il milione mentre su un albero bilanciato. Ci vogliono solo 20 visite! Questa è una differenza enorme!

Solveremo questo problema nel prossimo post usando alberi auto-bilanciati (alberi AVL).

Riassunto

Abbiamo coperto molto terreno per gli alberi. Riassumiamo con dei punti:

• L’albero è una struttura dati dove un nodo ha 0 o più discendenti/figli.
• I nodi dell’albero non hanno cicli (aciclici). Se ha cicli, è invece una struttura dati Graph.
• Gli alberi con due figli o meno sono chiamati: Albero Binario
• Quando un Albero Binario è ordinato in modo che il valore a sinistra sia minore del genitore e i figli a destra siano maggiori, allora e solo allora abbiamo un Albero di Ricerca Binario.
• Puoi visitare un albero in modo pre/post/in-order.
• Un albero sbilanciato ha una complessità temporale di O(n). 🤦🏻
• Un equilibrato ha una complessità temporale di O(log n). 🎉