Fysische chemie is een nogal breed onderwerp; het omvat:

• Kwantumchemie
• Thermochemie (Review + More)
• Kinetica (Review + More)
• Statistische mechanica

Omdat er nogal wat onderwerpen zijn voor één antwoord, zal ik slechts twee voorbeelden per onderwerp geven. Dit wordt een lang antwoord, maar je kunt je concentreren op wat je zoekt.

QUANTUM CHEMISTRY

Quantumchemie gaat over het algemeen over het proberen te begrijpen van scenario’s op de picoscopische schaal, het modelleren van systemen in handige wiskundige representaties en het maken van de juiste benaderingen.

Twee voorbeelden van kwantumchemie zijn:

• Eenvoudige harmonische oscillator (twee ballen verbonden door een ideale veer)

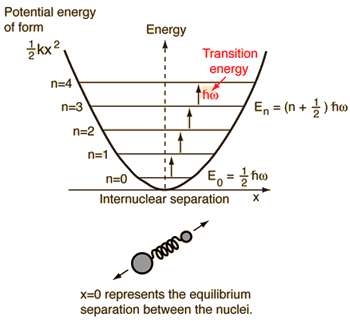
Voor dit systeem, dat we kennen uit de natuurkunde, reduceren we het van een klassiek tweelichamenprobleem tot een éénlichamenprobleem met relatieve coördinaten en een gereduceerde massa, #mu = (m_1m_2)/(m_1 + m_2)#.

Dit systeem is gericht op het begrijpen van de elastische potentiële energie van de moleculaire binding.

• Stijve rotor (twee ballen verbonden door een staaf, d.w.z. 100% stijve veer)

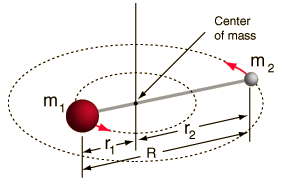
Dit systeem is een vereenvoudiging, aangezien alle moleculen een of andere vorm van uitrekking/trilling van de binding hebben (u zou begrijpen waarom deze vereenvoudiging OK is, als u de wiskunde zag!).

Hoewel, het stelt ons in staat om deze hoekcomponent van een tweelichamensysteem te ontleden en de rotatie-eigenschappen van het molecuul te begrijpen.

THERMOCHEMISTRY

Dit kijkt naar de macroscopische schaal van warmtestroom, arbeid, vrije energieën, enzovoorts. Je hebt dit al eerder gedaan in de algemene scheikunde enigszins, en dit wordt herzien en uitgebreid.

Twee voorbeelden zijn:

• Determining Thermodynamic Values from Measurable Quantities

Wat is scheikunde als het niet praktisch is?

Dus een rode draad is het kunnen uitvoeren van afleidingen en het kunnen uitdrukken van de belangrijkste thermodynamische grootheden (entropie, enthalpie, gibbs + helmholtz vrije energie, inwendige energie) in termen van natuurlijke grootheden als volume, temperatuur en druk.

Zo kan men bijvoorbeeld de entropie berekenen van een isotherme expansie (#DeltaT = 0, DeltaV > 0#) door #V_2# en #V_1# te kennen, of #P_2# en #P_1#, en dat voor een mono-atomair ideaal gas:

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Ideale en niet-ideale niet-elektrolyt/elektrolyt-oplossingen

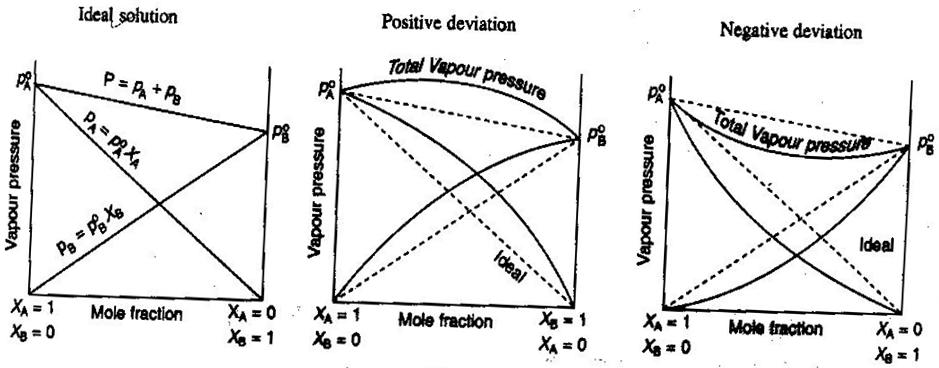
In de algemene scheikunde, behandelen we oplossingen graag ideaal, zodat volumes additief zijn, concentraties van sterke elektrolyten rechte #”mol/L “# berekeningen zijn, enzovoort. Enkele manieren waarop oplossingen niet ideaal kunnen zijn:

• De oplossing kan uitzetten of inkrimpen na te zijn gemengd.
• Ion pairing vermindert de ionische sterkte van de oplossing en verlaagt de van’t Hoff factor #i# van het opgeloste.
• De ontsnappingsneiging van de opgeloste stof verandert zijn effectieve concentratie (zijn activiteit).

KINETIEK

Je hebt dit misschien al eerder gedaan in een algemene scheikundeles, of misschien op de middelbare school. Fysische scheikunde gaat hier wat dieper op in door reactiemechanismen en gasfase-dynamica meer in detail te bekijken.

Twee voorbeelden:

• Steady-State benadering

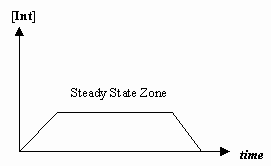
Soms is de snelheid van de eerste mechanistische stap veel langzamer dan die van de tweede stap, en we benaderen dat de concentratie van het tussenproduct effectief niet verandert (#(d)/(dt) = 0#).

Dat maakt het mogelijk om een snelheidswet af te leiden die specifiek is voor een mechanisme, en om een “waargenomen snelheidsconstante” uit te drukken in termen van de snelheidsconstanten voor de afzonderlijke stappen.

• Reële gaswetten

U hebt wellicht kennis gemaakt met de van der Waals toestandsvergelijking:

#(V – nb) = nRT#

Er zijn nog enkele andere, zoals de Redlich-Kwong, de Peng-Robinson, enzovoort.

Het basisidee is dat ze allemaal beter werken voor bepaalde gassen dan voor andere, maar ze werken allemaal om rekening te houden met de echte eigenschappen van gassen in plaats van aan te nemen dat iedereen een elastisch-botsende inerte puntmassa is.

STATISTISCHE MECHANIEK

Met statistische mechanica doen we een stap terug en bekijken we de picoscopische wereld vanuit een macroscopisch perspectief:

“Wat kunnen we van een systeem leren als we denken als een kwantumchemicus over een grote verzameling deeltjes?”

Twee voorbeelden:

• Equipartitietheorema

#<< K >> = N/2nRT = N/2 k_BT#,

waarbij #N# het aantal vrijheidsgraden is voor elk type beweging (lineair, roterend, trillend, elektronisch, nucleair). In principe wordt elk type beweging in een molecuul in aanmerking genomen om de gemiddelde kinetische energie ervan te schatten, #<< K >>#.

Dit werkt alleen bij temperaturen die “hoog genoeg” zijn. Gewoonlijk is het OK voor translatie- en rotatiebewegingen, maar het heeft de neiging om vibratiebijdragen te overschatten.

• De Microcanonieke Verdeelfunctie

#q = som_(i=1)^(N) g_ie^(-beta epsilon_i)#,

waar:

• #g_i# is de ontaarding van toestand #i# met energie #epsilon_i#.
• #N# is het totaal aantal beschikbare toestanden.

Net zoals de golffunctie #psi# alles specificeert wat er te weten valt over een kwantummechanisch systeem, specificeert de microcanonieke verdelingsfunctie hoe een molecuul zijn beschikbare energie kan verdelen over de mogelijke soorten toestanden (translatie-, rotatie-, vibratie-, elektronische en nucleaire toestanden).

Er bestaat een #q# voor elk type toestand: #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)#, en #q_(n uc)#.

Vanuit het kennen van elk type #q#, kunnen de bekende thermodynamische grootheden worden afgeleid, zoals entropie (#S#), enthalpie (#H#), vrije energie van Gibbs (#G#), enzovoort, in termen van elk soort #q#.

Als een nuttig voorbeeld kan de absolute moleculaire entropie bij ELKE temperatuur in de meeste gevallen worden berekend als:

#S/N = k_B ln (q/N)_”tot” + (<< epsilon >>_”tot”)/T + k_B#,

waar:

• #k_B ~~ “0.695 cm”^(-1)”/K “# de constante van Boltzmann is.
• #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# de totale microcanonieke verdelingsfunctie is die alle mogelijke soorten toestanden omvat, en #N# het totale aantal beschouwde moleculen is.
• #<< epsilon >> = E/N# is de moleculaire energie, gedefinieerd als #<< epsilon >> = k_BT^2((del ln (q”/”N)_”tot”)/(del T))_V#.

(Ja, met deze formule bij #”298.15 K “# kunt u dezelfde #S^@# berekenen die u in de bijlage van uw tekstboek ziet!)

Een voorbeeld van deze formule in gebruik vindt u hier.