Química Física é um pouco de um tópico amplo; cobre:

• Química Quântica
• Termochequímica (Revisão + Mais)
• Cinética (Revisão + Mais)
• Mecânica Estatística

Posto que existem alguns tópicos para uma resposta, vou apenas fornecer dois exemplos por tópico. Esta será uma resposta longa, mas você pode se concentrar no que está procurando.

QUANTUM CHEMISTRY

Quantum chemistry is generally about trying to understand scenarios on the picoscopic scale, modeling systems in convenient mathematical representations and making the appropriate approximations.

Dois exemplos de química quântica são:

• Oscilador harmónico simples (duas bolas ligadas por uma mola ideal)

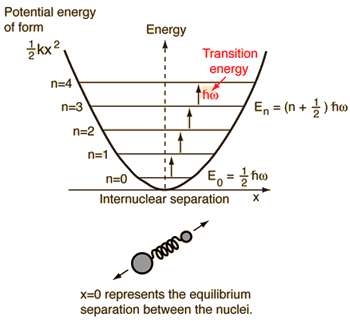
Para este sistema, que conhecemos pela física, reduzimo-lo de um problema clássico de dois corpos para um problema de um corpo com coordenadas relativas e massa reduzida, #mu = (m_1m_2)/(m_1 + m_2)#.

Este sistema foca-se na compreensão da energia potencial elástica da ligação molecular.

• Rotor rígido (duas esferas ligadas por uma haste, ou seja, 100% de mola rígida)

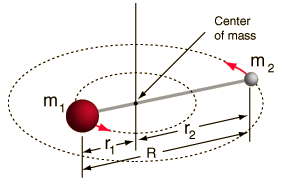
Este sistema é uma simplificação, pois todas as moléculas têm alguma forma de estiramento/vibração da ligação (você entenderia porque esta simplificação é OK, se você visse a matemática!).

Contudo, permite-nos decompor este componente angular de um sistema de dois corpos e compreender as propriedades rotacionais da molécula.

THERMOCHEMISTRY

Esta análise analisa a escala macroscópica do fluxo de calor, trabalho, energias livres, e assim por diante. Você já fez isso antes em química geral um pouco, e isso é revisto e expandido.

Dois exemplos são:

• Determinando Valores Termodinâmicos a partir de Quantidades Mensuráveis

O que é química se não é prática?

Então, um tema comum é ser capaz de realizar derivações e expressar as principais grandezas termodinâmicas (entropia, entalpia, gibbs + energia livre de helmholtz, energia interna) em termos de variáveis naturais como volume, temperatura e pressão.

Por exemplo, pode-se calcular a entropia a partir de uma expansão isotérmica (#DeltaT = 0, DeltaV > 0#) sabendo #V_2# e #V_1#, ou #P_2# e #P_1#, e isso para um gás ideal monatômico:

>

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Soluções não ideais não-eletrólitos/Electrolitos

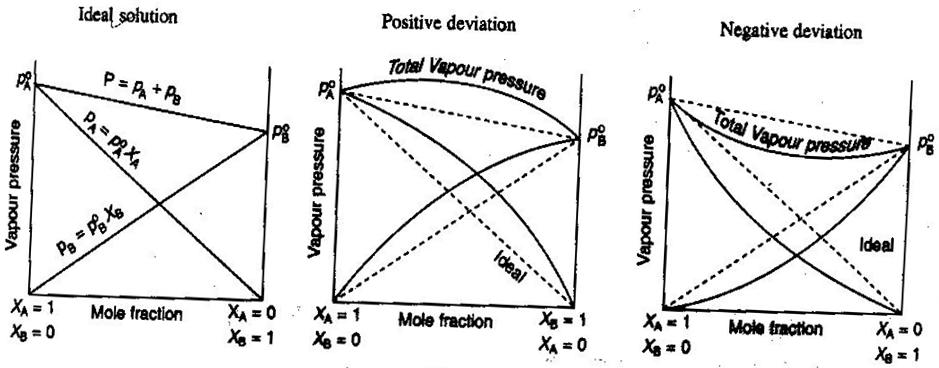
>Em química geral, nós gostamos de tratar soluções de forma ideal, para que os volumes sejam aditivos, as concentrações de electrólitos fortes sejam cálculos rectos #”mol/L “#, e assim por diante. Algumas formas que as soluções podem não ser ideais:

• A solução pode expandir ou contrair após ser misturada.
• O emparelhamento iónico diminui a força iónica da solução e reduz o factor van’t Hoff #i# do soluto.
• A tendência de fuga do soluto altera a sua concentração efectiva (a sua actividade).

KINÉTICA

Pode ter feito isto antes numa aula de química geral, ou talvez na escola secundária. A química física se expande um pouco mais, observando com mais detalhes os mecanismos de reação e a dinâmica da fase gasosa.

Dois exemplos:

• Proximação do estado estacionário

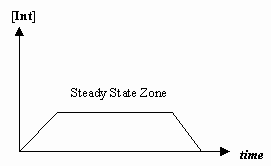
Algumas vezes a taxa do primeiro passo mecanicista é muito mais lenta que a do segundo passo, e aproximamos que a concentração do intermediário efetivamente não muda (#(d)/(dt) = 0#).

Que permite a derivação de uma lei de taxa particular para um mecanismo, e para nós expressarmos uma “constante de taxa observada” em termos das constantes de taxa para os passos individuais.

• Real Gas Laws

Pode ter sido introduzido à equação de estado van der Waals:

#(V – nb) = nRT#

Bem, há alguns outros, como o Redlich-Kwong, o Peng-Robinson, e assim por diante.

A ideia básica é que todos eles trabalham melhor para certos gases do que outros, mas todos eles trabalham para ter em conta as propriedades reais dos gases, em vez de assumir que todos são uma massa de ponto inerte elasticamente colidida.

MECÂNICA ESTATÍSTICA

Com mecânica estatística, damos um passo atrás e olhamos para o mundo picoscópico de uma perspectiva macroscópica:

“O que se pode aprender de um sistema se pensarmos como um químico quântico sobre uma grande coleção de partículas?”

Dois exemplos:

• Teoria da equipartição

####1147>< K >> = N/2nRT = N/2 k_BT#,

onde #N# é o número de graus de liberdade para cada tipo de movimento (linear, rotacional, vibracional, eletrônico, nuclear). Basicamente, leva em consideração cada tipo de movimento em uma molécula para estimar sua energia cinética média, #<< K >>#.

Isto só funciona a temperaturas “suficientemente altas”. Normalmente, é OK para movimentos translacionais e rotacionais, mas tende a sobrestimar as contribuições vibracionais.

• A Função de Partição Microcanónica

#q = soma_(i=1)^(N) g_ie^(-beta epsilon_i)#,

where:

• #g_i# é a degenerescência do estado #i# com energia #epsilon_i#.
• #N# é o número total de estados disponíveis.

Apenas como a função de onda #psi# especifica tudo o que há para saber sobre um sistema mecânico quântico, a função de partição microcanônica especifica como uma molécula pode distribuir sua energia disponível nos possíveis tipos de estados (translacional, rotacional, vibracional, eletrônico e nuclear).

Existe um #q# para cada tipo de estado: #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)#, e #q_(n uc)#.

Do conhecimento de cada tipo de #q#, as quantidades termodinâmicas familiares podem ser derivadas, tais como entropia (#S#), entalpia (#H#), energia livre de Gibbs (#G#), e assim por diante, em termos de cada tipo de #q#.

Como exemplo útil, a entropia molecular absoluta a QUALQUER temperatura na maioria dos casos pode ser calculada como:

#S/N = k_B ln (q/N)_”tot” + (<< epsilon >>_”tot”)/T + k_B#,

where:

• #k_B ~~ “0.695 cm”^(-1)”/K “# é a constante de Boltzmann.
• #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# é a função de partição microcanônica total que inclui todos os tipos possíveis de estados, e #N# é o número total de moléculas consideradas.
• #<< epsilon >> = E/N# é a energia molecular, definida como #<< epsilon >> = k_BT^2((del ln (q”/”N)_”tot”)/(del T))_V#.

(Sim, esta fórmula em #”298.15 K “# permite calcular o mesmo #S^@# que você vê no apêndice do seu livro didático!)

Um exemplo desta fórmula em uso pode ser encontrado aqui.