Fyzikální chemie je poněkud široké téma; zahrnuje:

• Kvantovou chemii
• Termochemii (přehled + další)
• Kinetiku (přehled + další)
• Statistickou mechaniku

Protože témat je na jednu odpověď poměrně málo, uvedu pouze dva příklady na téma. Bude to dlouhá odpověď, ale můžete se zaměřit na to, co hledáte.

KVANTOVÁ CHEMIE

Kvantová chemie je obecně o snaze pochopit scénáře v pikoskopickém měřítku, modelování systémů ve vhodných matematických reprezentacích a provádění příslušných aproximací.

Dvěma příklady kvantové chemie jsou:

• Jednoduchý harmonický oscilátor (dvě kuličky spojené ideální pružinou)

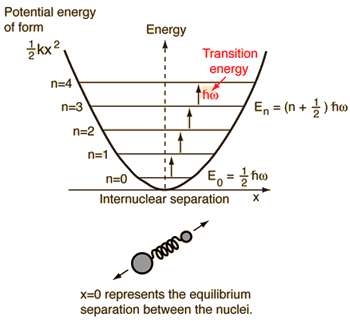
Pro tento systém, který známe z fyziky, jej redukujeme z klasického problému dvou těles na problém jednoho tělesa s relativními souřadnicemi a redukovanou hmotností, #mu = (m_1m_2)/(m_1 + m_2)#.

Tento systém se zaměřuje na pochopení elastické potenciální energie molekulární vazby.

• Tuhý rotor (dvě kuličky spojené tyčí, tj. 100% tuhá pružina)

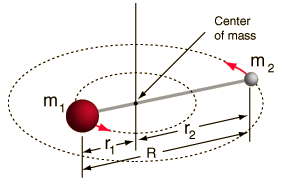
Tato soustava je zjednodušením, protože všechny molekuly mají nějakou formu roztažení/vibrace vazby (pochopili byste, proč je toto zjednodušení v pořádku, kdybyste viděli matematiku!).

Umožňuje nám však rozložit tuto úhlovou složku soustavy dvou těles a pochopit rotační vlastnosti molekuly.

THERMOCHEMIE

Tato se zabývá makroskopickým měřítkem tepelného toku, práce, volných energií atd. To jste již v obecné chemii poněkud probírali a je to zopakováno a rozšířeno.

Dva příklady jsou:

• Určení termodynamických hodnot z měřitelných veličin

Co je to za chemii, když není praktická?

Takže společným tématem je umět provádět derivace a vyjádřit hlavní termodynamické veličiny (entropie, entalpie, gibbsova + helmholtzova volná energie, vnitřní energie) v termínech přirozených veličin, jako je objem, teplota a tlak.

Například entropii lze vypočítat z izotermické expanze (#DeltaT = 0, DeltaV > 0#), když známe #V_2# a #V_1# nebo #P_2# a #P_1#, a to pro monatomický ideální plyn:

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Ideální a neideální roztoky neelektrolytů/elektrolytů

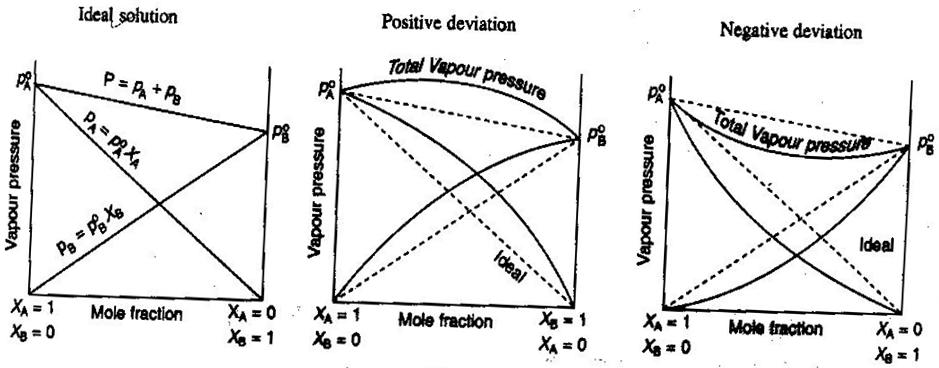
V obecné chemii, rádi zacházíme s roztoky ideálně, takže objemy jsou aditivní, koncentrace silných elektrolytů jsou přímé výpočty #“mol/l „# a tak dále. Některé způsoby, jak roztoky nemusí být ideální:

• Roztok se může po smíchání rozpínat nebo smršťovat.
• Spojování iontů snižuje iontovou sílu roztoku a snižuje van’t Hoffův faktor #i# rozpuštěné látky.
• Úniková tendence rozpuštěné látky mění její efektivní koncentraci (její aktivitu).

KINETIKA

Možná jste to už někdy dělali v hodinách obecné chemie nebo možná na střední škole. Fyzikální chemie to trochu více rozšiřuje tím, že se podrobněji zabývá reakčními mechanismy a dynamikou plynné fáze.

Dva příklady:

• Aproximace ustáleného stavu

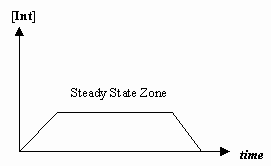
Někdy je rychlost prvního mechanistického kroku mnohem pomalejší než rychlost druhého kroku a aproximujeme, že koncentrace meziproduktu se efektivně nemění (#(d)/(dt) = 0#).

To umožňuje odvodit rychlostní zákon specifický pro daný mechanismus a vyjádřit „pozorovanou rychlostní konstantu“ pomocí rychlostních konstant pro jednotlivé kroky.

• Reálné plynové zákony

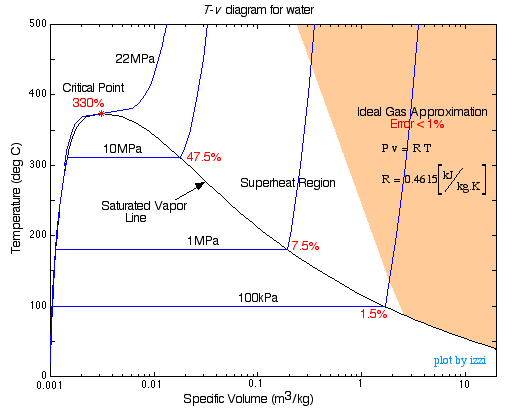
Možná jste se seznámili s van der Waalsovou stavovou rovnicí:

#(V – nb) = nRT#

No a existují i některé další, například Redlichova-Kwongova, Pengova-Robinsonova atd.

Základní myšlenka je, že všechny fungují pro určité plyny lépe než jiné, ale všechny fungují tak, aby zohlednily skutečné vlastnosti plynů, místo aby předpokládaly, že každý je pružně se srážející inertní bodová hmota.

STATISTICKÁ MECHANIKA

Při statistické mechanice uděláme krok zpět a podíváme se na pikosvět z makroskopické perspektivy:

„Co se můžeme ze systému dozvědět, pokud o velkém souboru částic uvažujeme jako kvantový chemik?“

Dva příklady:

• Věta o rozdělení

#<< K >> = N/2nRT = N/2 k_BT#,

kde #N# je počet stupňů volnosti pro každý typ pohybu (lineární, rotační, vibrační, elektronický, jaderný). V podstatě se bere v úvahu každý typ pohybu v molekule, aby se odhadla její průměrná kinetická energie, #<< K >>#.

To funguje pouze při „dostatečně vysokých“ teplotách. Obvykle je to v pořádku pro translační a rotační pohyby, ale má tendenci nadhodnocovat vibrační příspěvky.

• Mikrokanonická rozdělovací funkce

#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)#,

kde:

• #g_i# je degenerace stavu #i# s energií #epsilon_i#.
• #N# je celkový počet dostupných stavů.

Stejně jako vlnová funkce #psi# určuje vše, co je třeba vědět o kvantově mechanickém systému, mikrokanonická rozdělovací funkce určuje, jak může molekula rozdělit svou dostupnou energii do možných typů stavů (translační, rotační, vibrační, elektronický a jaderný).

Pro každý typ stavu existuje #q#:

Znalost každého typu #q# umožňuje odvodit známé termodynamické veličiny, jako je entropie (#S#), entalpie (#H#), Gibbsova volná energie (#G#) atd., z hlediska každého typu #q#.

Jako užitečný příklad lze absolutní molekulovou entropii při JAKÉKOLI teplotě ve většině případů vypočítat jako:

#S/N = k_B ln (q/N)_“tot“ + (<< epsilon >>_“tot“)/T + k_B#,

kde:

• #k_B ~~“0.695 cm“^(-1)“/K „# je Boltzmannova konstanta.
• #(q/N)_“tot“ = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# je celková mikrokanonická rozdělovací funkce, která zahrnuje všechny možné typy stavů, a #N# je celkový počet uvažovaných molekul.
• #<< epsilon >> = E/N# je molekulová energie definovaná jako #<< epsilon >> = k_BT^2((del ln (q“/“N)_“tot“)/(del T))_V#.

(Ano, tento vzorec při #“298,15 K „# umožňuje vypočítat stejný #S^@#, který vidíte v příloze učebnice!)

Příklad použití tohoto vzorce najdete zde.

.