Trædatastrukturer har mange anvendelsesmuligheder, og det er godt at have en grundlæggende forståelse af, hvordan de fungerer. Træer er grundlaget for andre meget anvendte datastrukturer som Maps og Sets. De bruges også på databaser til at udføre hurtige søgninger. HTML DOM bruger en trædatastruktur til at repræsentere elementernes hierarki. Dette indlæg vil udforske de forskellige typer af træer som binære træer, binære søgetræer, og hvordan man implementerer dem.

Vi udforskede Graph-datastrukturer i det foregående indlæg, som er et generaliseret tilfælde af træer. Lad os komme i gang med at lære, hvad trædatastrukturer er!

Dette indlæg er en del af en tutorial-serie:

Læring af datastrukturer og algoritmer (DSA) for begyndere

1. Intro til algoritmers tidskompleksitet og Big O notation

2. Otte tidskompleksiteter, som enhver programmør bør kende

3. Datastrukturer for begyndere: Arrays, HashMaps og lister

4. Grafiske datastrukturer for begyndere

5. Træer Datastrukturer for begyndere 👈 du er her

6. Selvafbalancerede binære søgetræer

7. Appendiks I: Analyse af rekursive algoritmer

Træer: grundlæggende begreber

Et træ er en datastruktur, hvor en knude kan have nul eller flere børn. Hver knude indeholder en værdi. Ligesom grafer kaldes forbindelsen mellem knuder for kanter. Et træ er en type graf, men ikke alle grafer er træer (mere om det senere).

Disse datastrukturer kaldes “træer”, fordi datastrukturen ligner et træ 🌳. Den starter med en rodknude og forgrener sig med dens efterkommere, og til sidst er der blade.

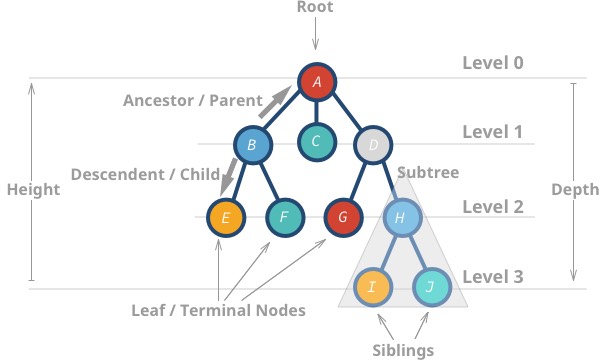
Her er nogle egenskaber ved træer:

• Den øverste knude kaldes rod.
• En knude uden børn kaldes bladknude eller terminalknude.
• Træets højde (h) er afstanden (antallet af kanter) mellem det fjerneste blad og roden.
  • A A har en højde på 3
  • I har en højde på 0
• En knudes dybde eller niveau er afstanden mellem roden og den pågældende knude.
  • H har en dybde på 2
  • B har en dybde på 1

Implementering af en simpel trædatastruktur

Som vi så tidligere, er en træknude blot en datastruktur med en værdi og links til dens efterkommere.

Her er et eksempel på en træknude:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Vi kan oprette et træ med 3 efterkommere på følgende måde:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Det var det hele; vi har en trædatastruktur!

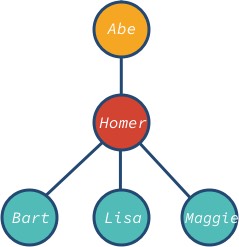
Noden abe er roden, og bart, lisa og maggie er bladknuderne i træet. Bemærk, at træets knude kan have forskellige efterkommere: 0, 1, 3 eller en hvilken som helst anden værdi.

Træ-datastrukturer har mange anvendelsesmuligheder, f.eks.:

• Kort
• Sæt
• Databaser
• Prioritetskøer
• Søgning af en LDAP (Lightweight Directory Access Protocol)
• Repræsentation af Document Object Model (DOM) for HTML på websteder.

Binære træer

Træernes knuder kan have nul eller flere børn. Men når et træ højst har to børn, kaldes det binært træ.

Fuldt, fuldstændigt og perfekt binært træ

Afhængigt af, hvordan knuderne er arrangeret i et binært træ, kan det være fuldt, fuldstændigt og perfekt:

• Fuldt binært træ: Hver knude har præcis 0 eller 2 børn (men aldrig 1).
• Komplet binært træ: Når alle niveauer undtagen det sidste er fyldt med knuder.
• Perfekt binært træ: Når alle niveauer (inklusive det sidste) er fyldt med knuder.

Se disse eksempler:

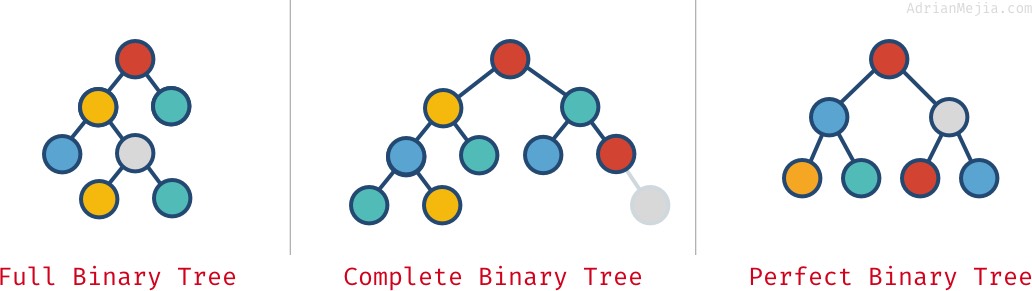
Disse egenskaber udelukker ikke altid hinanden. Man kan have mere end én:

• Et perfekt træ er altid komplet og fuldt.
  • Perfekte binære træer har præcis `2^k – 1` knuder, hvor k er det sidste niveau i træet (begyndende med 1).
• Et komplet træ er ikke altid full.
  • Som i vores “komplette” eksempel, da det har en forælder med kun ét barn. Hvis vi fjerner den grå knude længst til højre, vil vi have et komplet og fuldt træ, men ikke perfekt.
• Et fuldt træ er ikke altid komplet og perfekt.

Binary Search Tree (BST)

Binary Search Trees eller forkortet BST er en særlig anvendelse af binære træer. BST har højst to knuder (som alle binære træer). Værdierne er dog således, at venstre børns værdi skal være mindre end forældrenes, og højre børns værdi skal være højere.

Duplikater: Nogle BST tillader ikke dubletter, mens andre tilføjer de samme værdier som et højre barn. Andre implementeringer kan holde en optælling på et tilfælde af duplicitet (vi kommer til at gøre dette senere).

Lad os implementere et binært søgetræ!

BST-implementering

BST ligner meget vores tidligere implementering af et træ. Der er dog nogle forskelle:

• Noder kan højst have to børn: venstre og højre.
• Nodernes værdier skal være ordnet som left < parent < right.

Her er træets node. Meget lig det, vi gjorde før, men vi har tilføjet nogle praktiske getters og setters for venstre og højre børn. Bemærk holder også en reference til forældrene, og vi opdaterer den, hver gang vi tilføjer børn.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Ok, indtil videre kan vi tilføje et venstre og et højre barn. Lad os nu lave BST-klassen, der håndhæver left < parent < right-reglen.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Lad os implementere indsættelse.

BST Node Insertion

For at indsætte en node i et binært træ gør vi følgende:

1. Hvis et træ er tomt, bliver den første node roden, og du er færdig.
2. Sammenlign rodens/forældrenes værdi, hvis den er højere, gå til højre, hvis den er lavere, gå til venstre. Hvis det er det samme, findes værdien allerede, så du kan øge antallet af dubletter (multiplicitet).
3. Gentag #2, indtil vi har fundet en tom plads til at indsætte den nye knude.

Lad os lave en illustration af, hvordan man indsætter 30, 40, 10, 15, 12, 50:

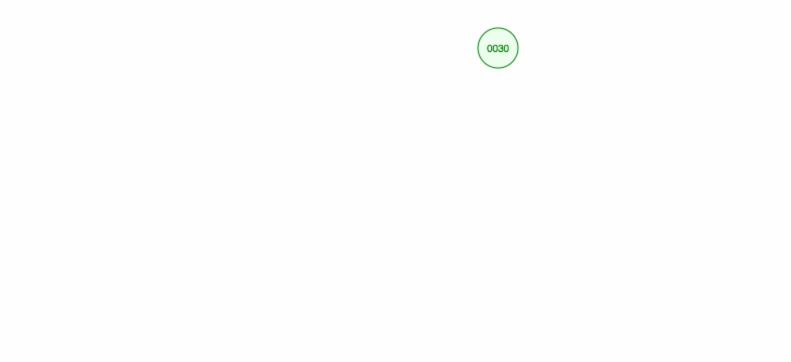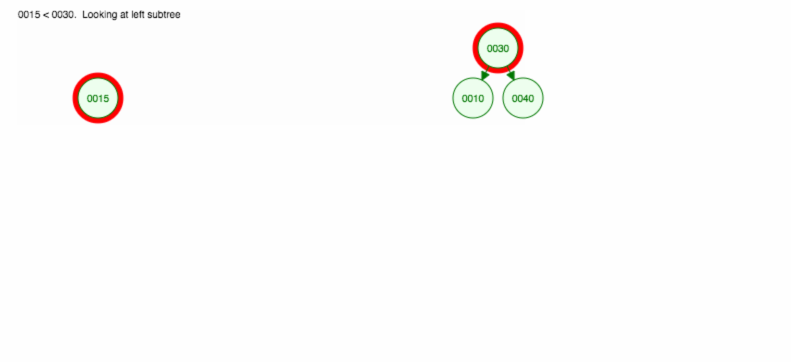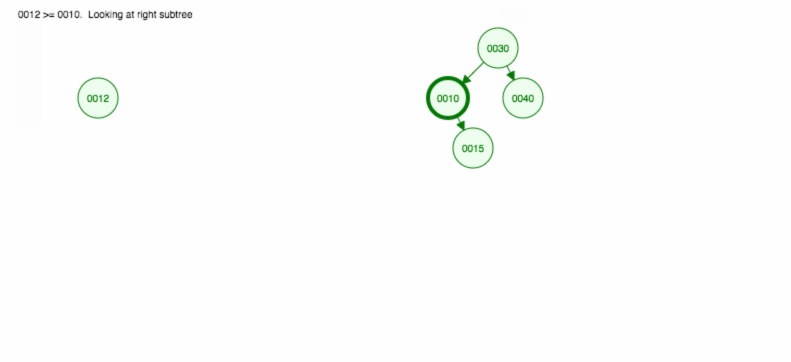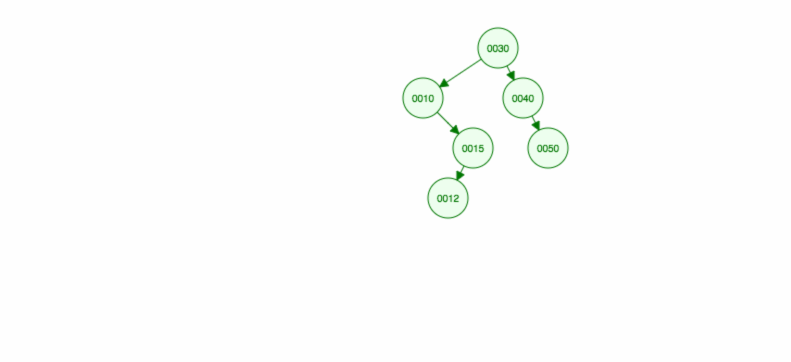
Vi kan implementere indsættelse på følgende måde:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Vi bruger en hjælpefunktion ved navn findNodeAndParent. Hvis vi har fundet ud af, at noden allerede findes i træet, øger vi tælleren multiplicity. Lad os se, hvordan denne funktion er implementeret:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent går igennem træet og leder efter værdien. Den starter ved roden (linje 2) og går derefter til venstre eller højre baseret på værdien (linje 10). Hvis værdien allerede findes, returnerer den knuden found og også den overordnede knude. Hvis noden ikke findes, returnerer vi stadig parent.

BST Node Deletion

Vi ved, hvordan man indsætter og søger efter værdi. Nu skal vi implementere sletningsoperationen. Det er lidt vanskeligere end at tilføje, så lad os forklare det med følgende tilfælde:

Sletning af en bladnode (0 børn)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Vi fjerner referencen fra nodens forælder (15) til at være nul.

Sletning af en node med ét barn.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

I dette tilfælde går vi til forældrene (30) og erstatter barnet (10) med et barns barn (15).

Sletning af en node med to børn

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Vi fjerner node 40, som har to børn (35 og 50). Vi erstatter forældrenes (30) barn (40) med barnets højre barn (50). Derefter beholder vi det venstre barn (35) samme sted som før, så vi skal gøre det til venstre barn af 50.

En anden måde at fjerne node 40 på er at flytte det venstre barn (35) op og derefter beholde det højre barn (50), hvor det var.

1
2
3
4
5

 30
/ \
15 35
\
50

Enten måde er ok, så længe du beholder den binære søgetræ-egenskab: left < parent < right.

Sletning af roden.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Sletning af roden svarer meget til at fjerne knuder med 0, 1 eller 2 børn, som blev diskuteret tidligere. Den eneste forskel er, at vi bagefter skal opdatere referencen til træets rod.

Her er en animation af det, vi diskuterede.

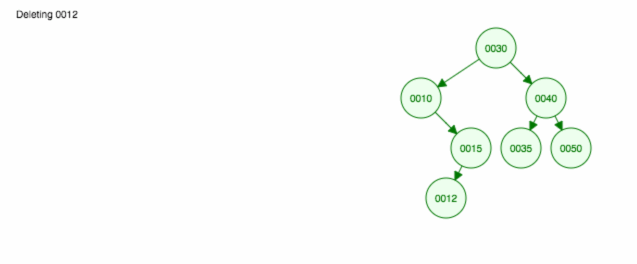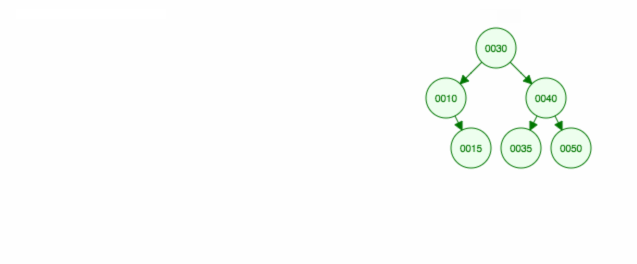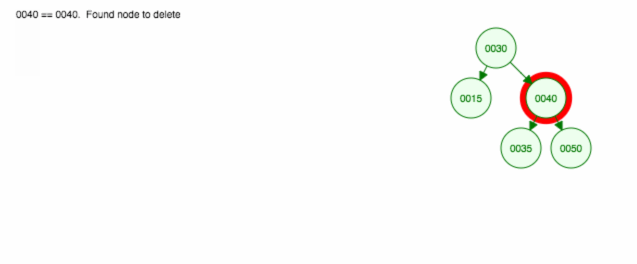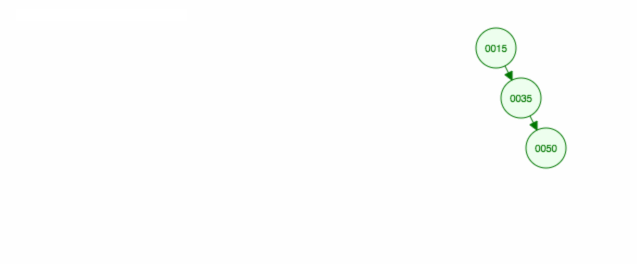
Animationen flytter det venstre barn/undertræ opad og holder det højre barn/undertræ på plads.

Nu da vi har en god idé om, hvordan det skal fungere, lad os implementere det:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Her er nogle højdepunkter i implementeringen:

• Først søger vi, om knuden findes. Hvis den ikke gør det, returnerer vi false, og vi er færdige!
• Hvis den node, der skal fjernes, findes, kombineres venstre og højre barn til ét undertræ.
• Forsæt node, der skal slettes, med det kombinerede undertræ.

Den funktion, der kombinerer venstre til højre undertræ, er følgende:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

For eksempel, lad os sige, at vi ønsker at kombinere følgende træ, og at vi er ved at slette knude 30. Vi ønsker at blande 30’s venstre undertræ til det højre undertræ. Resultatet bliver dette:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Hvis vi gør det nye undertræ til rod, så er knude 30 ikke længere!

Binary Tree Transversal

Der er forskellige måder at gennemløbe et binært træ på, afhængigt af den rækkefølge, som knuderne besøges i: in-order, pre-order og post-order. Vi kan også bruge demDFSogBFSsom vi lærte fra grafen post.Lad os gennemgå hver enkelt.

In-Order Traversal

In-order traversal besøger noder i denne rækkefølge: venstre, parent, right.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Lad os bruge dette træ til at lave eksemplet:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

In-order traversal would print out the following values: 3, 4, 5, 10, 15, 30, 40. Hvis træet er et BST, vil noderne blive sorteret i opstigende orden som i vores eksempel.

Post-Order Traversal

Post-Order traversal besøger noder i denne rækkefølge: venstre, højre, parent.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversal ville udskrive følgende værdier: 3, 4, 5, 15, 40, 30, 10.

Pre-Order Traversal and DFS

Pre-order traversal visit nodes on this order: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversal ville udskrive følgende værdier: 10, 5, 4, 3, 30, 15, 40. Denne rækkefølge af tal er det samme resultat, som vi ville få, hvis vi kørte DFS (Depth-First Search).

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Hvis du har brug for en genopfriskning af DFS, har vi dækket det i detaljer på Graph post.

Breadth-First Search (BFS)

I lighed med DFS kan vi implementere en BFS ved at skifte Stack ud med en Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

BFS-ordningen er: 10, 5, 30, 4, 15, 40, 3

Balancerede vs. ikke-balancerede træer

Så langt har vi diskuteret, hvordan man add, remove og find elementer. Vi har dog ikke talt om køretider. Lad os tænke på de værst tænkelige scenarier.

Lad os sige, at vi ønsker at tilføje tal i stigende rækkefølge.

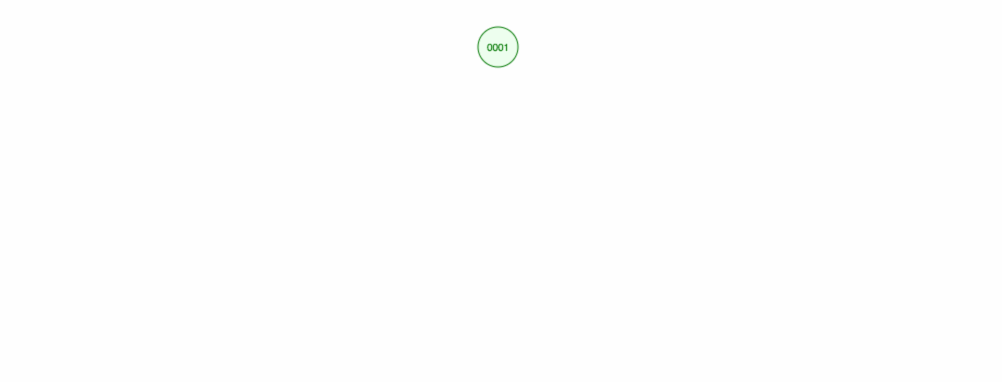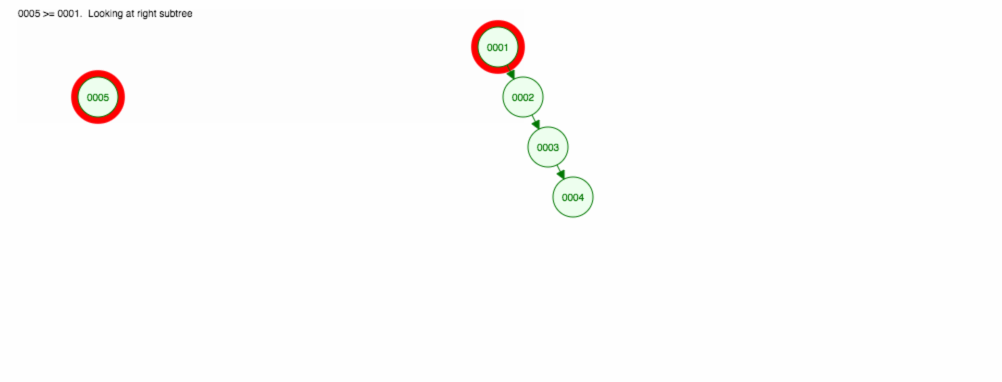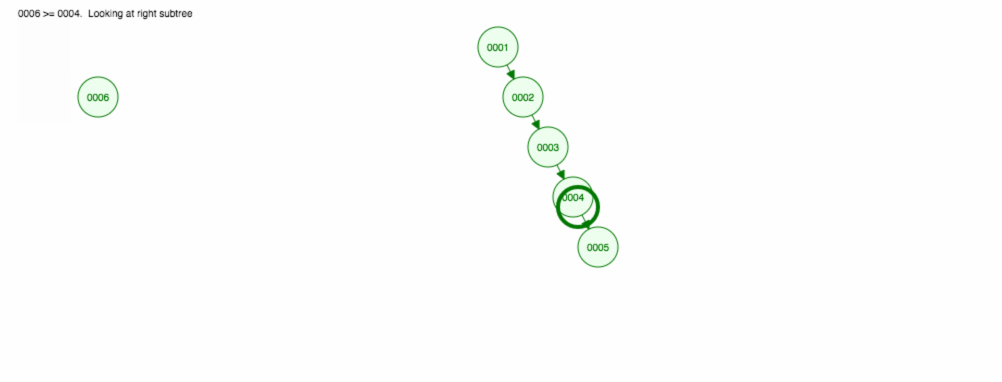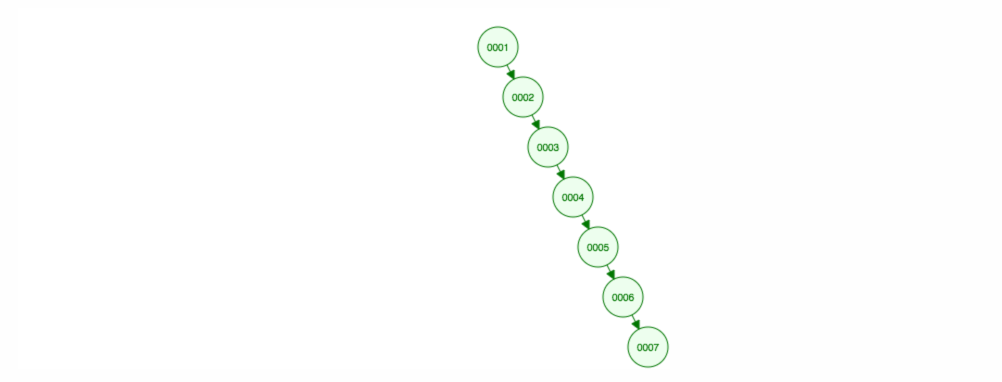
Vi vil ende med at få alle knuder på højre side! Dette ubalancerede træ er ikke bedre end en LinkedList, så det vil tage O(n) at finde et element. 😱

Søge efter noget i et ubalanceret træ er som at søge efter et ord i ordbogen side for side. Når træet er balanceret, kan man åbne ordbogen i midten, og derfra ved man, om man skal gå til venstre eller højre afhængigt af alfabetet og det ord, man leder efter.

Vi er nødt til at finde en måde at balancere træet på!

Hvis træet var balanceret, kunne vi finde elementer på O(log n) i stedet for at gå igennem hver enkelt knude. Lad os tale om, hvad et balanceret træ betyder.

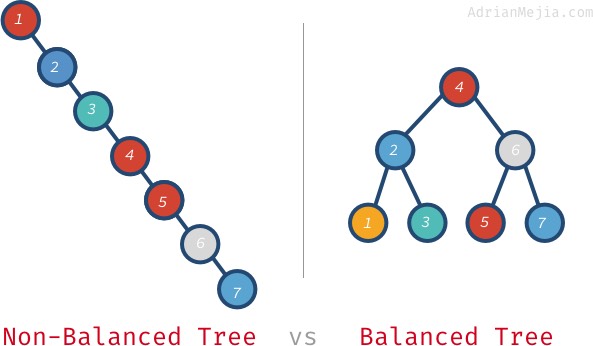
Hvis vi søger efter 7 i det ikke-balancerede træ, skal vi gå fra 1 til 7. Men i det balancerede træ besøger vi: 4, 6 og 7. Det bliver endnu værre med større træer. Hvis du har en million knuder, kan det for at søge efter et ikke-eksisterende element kræve, at du besøger alle millioner, mens du i et balanceret træ skal besøge alle millioner. Det kræver blot 20 besøg! Det er en enorm forskel!

Vi vil løse dette problem i det næste indlæg ved hjælp af selvbalancerede træer (AVL-træer).

Sammenfatning

Vi har dækket meget terræn for træer. Lad os opsummere det med bullets:

• Træet er en datastruktur, hvor en node har 0 eller flere efterkommere/børn.
• Træets noder har ikke cyklusser (acykliske). Hvis den har cyklusser, er det i stedet en Graph-datastruktur.
• Træer med to børn eller mindre kaldes: Binært træ
• Når et binært træ sorteres således, at den venstre værdi er mindre end forældrene og de højre børn er højere, så og kun så har vi et binært søgetræ.
• Du kan besøge et træ på en før/efter/in-ordnings måde.
• En ubalanceret har en tidskompleksitet på O(n). 🤦🏻
• En balanceret har en tidskompleksitet på O(log n). 🎉