Tree Data Structures haben viele Verwendungen, und es ist gut, ein grundlegendes Verständnis davon zu haben, wie sie funktionieren. Bäume sind die Grundlage für andere häufig verwendete Datenstrukturen wie Maps und Sets. Außerdem werden sie in Datenbanken verwendet, um eine schnelle Suche durchzuführen. Das HTML-DOM verwendet eine Baumdatenstruktur, um die Hierarchie der Elemente darzustellen. In diesem Beitrag werden die verschiedenen Arten von Bäumen, wie binäre Bäume und binäre Suchbäume, und deren Implementierung untersucht.

Im vorherigen Beitrag haben wir Graph-Datenstrukturen untersucht, die einen verallgemeinerten Fall von Bäumen darstellen. Lassen Sie uns nun lernen, was Baumdatenstrukturen sind!

Dieser Beitrag ist Teil einer Tutorial-Serie:

Erlernen von Datenstrukturen und Algorithmen (DSA) für Anfänger

1. Einführung in die Zeitkomplexität von Algorithmen und die Big O Notation

2. Acht Zeitkomplexitäten, die jeder Programmierer kennen sollte

3. Datenstrukturen für Anfänger: Arrays, HashMaps und Listen

4. Grafische Datenstrukturen für Anfänger

5. Bäume Datenstrukturen für Anfänger 👈 Sie sind hier

6. Selbstbalancierte binäre Suchbäume

7. Anhang I: Analyse rekursiver Algorithmen

Bäume: Grundbegriffe

Ein Baum ist eine Datenstruktur, bei der ein Knoten null oder mehr Kinder haben kann. Jeder Knoten enthält einen Wert. Wie bei Graphen werden die Verbindungen zwischen den Knoten als Kanten bezeichnet. Ein Baum ist eine Art von Graph, aber nicht alle Graphen sind Bäume (mehr dazu später).

Diese Datenstrukturen werden „Bäume“ genannt, weil die Datenstruktur einem Baum ähnelt 🌳. Er beginnt mit einem Wurzelknoten und verzweigt sich mit seinen Nachkommen, und schließlich gibt es Blätter.

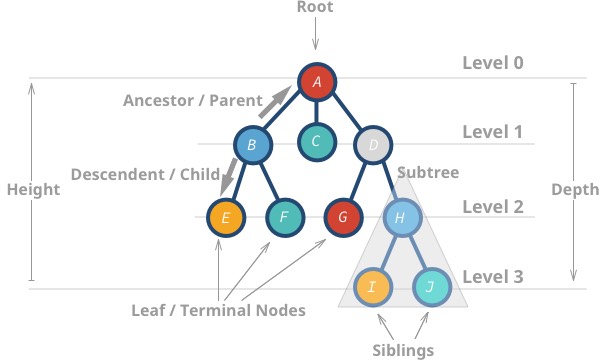
Hier sind einige Eigenschaften von Bäumen:

• Der oberste Knoten wird Wurzel genannt.
• Ein Knoten ohne Kinder wird Blattknoten oder Endknoten genannt.
• Die Höhe (h) des Baumes ist der Abstand (Anzahl der Kanten) zwischen dem am weitesten entfernten Blatt und der Wurzel.
  • A hat eine Höhe von 3
  • I hat eine Höhe von 0
• Die Tiefe oder Ebene eines Knotens ist der Abstand zwischen der Wurzel und dem betreffenden Knoten.
  • H hat eine Tiefe von 2
  • B hat eine Tiefe von 1

Implementieren einer einfachen Baumdatenstruktur

Wie wir bereits gesehen haben, ist ein Baumknoten nur eine Datenstruktur mit einem Wert und Links zu seinen Nachkommen.

Hier ist ein Beispiel für einen Baumknoten:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Wir können einen Baum mit 3 Nachkommen wie folgt erstellen:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Das ist alles; wir haben eine Baumdatenstruktur!

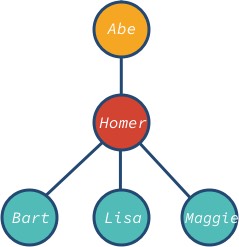
Der Knoten abe ist die Wurzel und bart, lisa und maggie sind die Blattknoten des Baums. Beachten Sie, dass die Knoten des Baums verschiedene Nachkommen haben können: 0, 1, 3 oder jeden anderen Wert.

Baumdatenstrukturen haben viele Anwendungen wie:

• Maps
• Sets
• Datenbanken
• Prioritätswarteschlangen
• Abfrage eines LDAP (Lightweight Directory Access Protocol)
• Darstellung des Document Object Model (DOM) für HTML auf Websites.

Binäre Bäume

Baumknoten können null oder mehr Kinder haben. Wenn ein Baum jedoch höchstens zwei Kinder hat, dann nennt man ihn Binärbaum.

Vollständige, komplette und perfekte Binärbäume

Abhängig davon, wie die Knoten in einem Binärbaum angeordnet sind, kann er vollständig, komplett und perfekt sein:

• Vollständiger Binärbaum: Jeder Knoten hat genau 0 oder 2 Kinder (aber niemals 1).
• Vollständiger Binärbaum: wenn alle Ebenen außer der letzten voll mit Knoten sind.
• Perfekter Binärbaum: wenn alle Ebenen (einschließlich der letzten) voll mit Knoten sind.

Sieh dir diese Beispiele an:

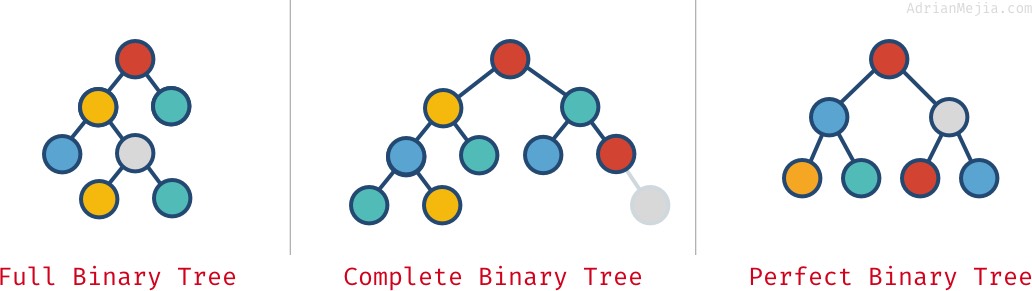
Diese Eigenschaften schließen sich nicht immer gegenseitig aus. Man kann mehr als eine haben:

• Ein perfekter Baum ist immer vollständig und voll.
  • Perfekte binäre Bäume haben genau `2^k – 1` Knoten, wobei k die letzte Ebene des Baumes ist (beginnend mit 1).
• Ein vollständiger Baum ist nicht immer full.
  • Wie in unserem „vollständigen“ Beispiel, da er ein Elternteil mit nur einem Kind hat. Wenn wir den ganz rechten grauen Knoten entfernen, dann hätten wir einen vollständigen und vollen Baum, aber nicht perfekt.
• Ein vollständiger Baum ist nicht immer vollständig und perfekt.

Binärer Suchbaum (BST)

Binäre Suchbäume oder kurz BST sind eine besondere Anwendung von binären Bäumen. BST hat höchstens zwei Knoten (wie alle binären Bäume). Die Werte sind jedoch so, dass der Wert des linken Kindes kleiner als der des Elternteils und der des rechten Kindes größer sein muss.

Duplikate: Einige BST lassen keine Duplikate zu, während andere die gleichen Werte als rechtes Kind hinzufügen. Andere Implementierungen könnten eine Zählung für den Fall einer Duplizität durchführen (wir werden dies später tun).

Lassen Sie uns einen binären Suchbaum implementieren!

BST-Implementierung

BST sind unserer vorherigen Implementierung eines Baumes sehr ähnlich. Es gibt jedoch einige Unterschiede:

• Knoten können höchstens zwei Kinder haben: links und rechts.
• Knotenwerte müssen als left < parent < right geordnet werden.

Hier ist der Baumknoten. Sehr ähnlich zu dem, was wir vorher gemacht haben, aber wir haben einige praktische Getter und Setter für linke und rechte Kinder hinzugefügt. Beachten Sie, dass wir auch einen Verweis auf das Elternteil behalten und ihn jedes Mal aktualisieren, wenn wir Kinder hinzufügen.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Ok, so weit können wir ein linkes und rechtes Kind hinzufügen. Jetzt machen wir die BST-Klasse, die die left < parent < right-Regel durchsetzt.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Lassen Sie uns das Einfügen implementieren.

Einfügen von BST-Knoten

Um einen Knoten in einen Binärbaum einzufügen, gehen wir wie folgt vor:

1. Wenn der Baum leer ist, wird der erste Knoten zur Wurzel, und man ist fertig.
2. Vergleiche den Wert von Wurzel und Elternteil, wenn er höher ist, gehe nach rechts, wenn er niedriger ist, gehe nach links. Wenn er gleich ist, dann existiert der Wert bereits, so dass du die Anzahl der Duplikate erhöhen kannst (Multiplizität).
3. Wiederhole #2, bis wir einen leeren Platz gefunden haben, um den neuen Knoten einzufügen.

Lassen Sie uns eine Illustration machen, wie man 30, 40, 10, 15, 12, 50 einfügt:

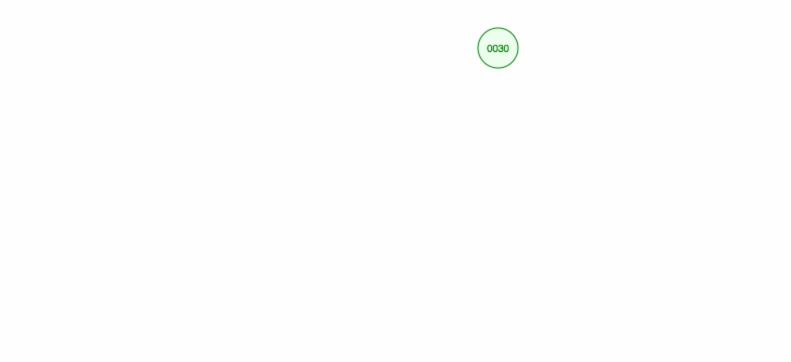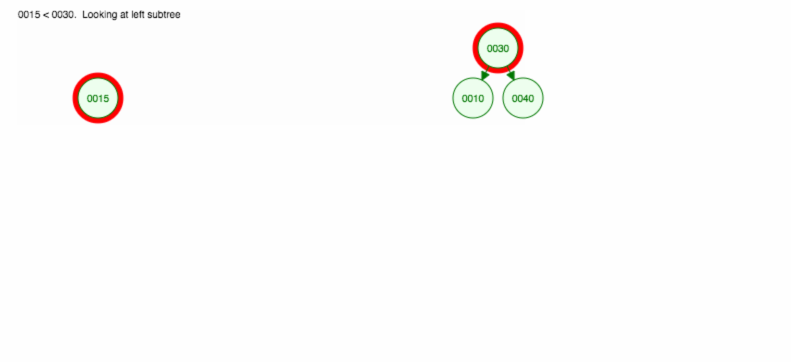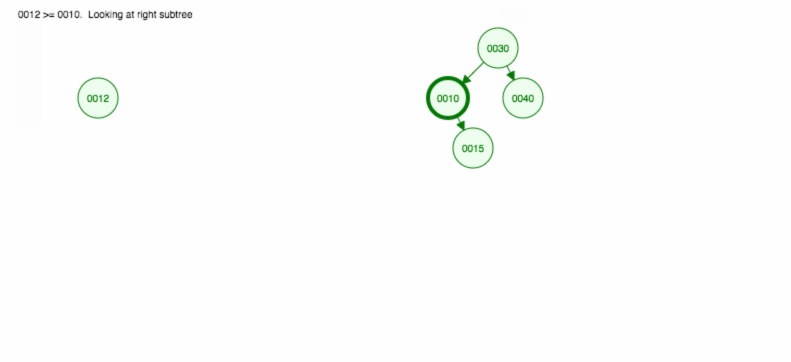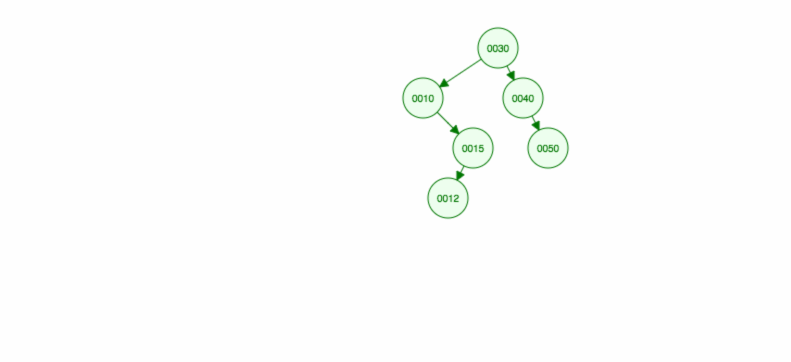
Wir können insert wie folgt implementieren:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Wir verwenden eine Hilfsfunktion namens findNodeAndParent. Wenn wir feststellen, dass der Knoten bereits im Baum existiert, erhöhen wir den multiplicity-Zähler. Sehen wir uns an, wie diese Funktion implementiert ist:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent geht durch den Baum und sucht nach dem Wert. Sie beginnt bei der Wurzel (Zeile 2) und geht dann je nach Wert nach links oder rechts (Zeile 10). Wenn der Wert bereits vorhanden ist, werden der Knoten found und auch der übergeordnete Knoten zurückgegeben. Falls der Knoten nicht existiert, wird immer noch parent zurückgegeben.

BST Node Deletion

Wir wissen, wie man Werte einfügt und sucht. Jetzt werden wir den Löschvorgang implementieren. Sie ist etwas kniffliger als das Hinzufügen, also erklären wir sie anhand der folgenden Fälle:

Löschen eines Blattknotens (0 Kinder)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Wir entfernen die Referenz vom Elternteil des Knotens (15), damit sie null ist.

Löschen eines Knotens mit einem Kind.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

In diesem Fall gehen wir zum Elternteil (30) und ersetzen das Kind (10) durch das Kind eines Kindes (15).

Löschen eines Knotens mit zwei Kindern

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Wir entfernen den Knoten 40, der zwei Kinder (35 und 50) hat. Wir ersetzen das übergeordnete Kind (30) des Knotens (40) durch das rechte Kind (50) des Knotens. Dann behalten wir das linke Kind (35) an der gleichen Stelle wie vorher, also müssen wir es zum linken Kind von 50 machen.

Eine andere Möglichkeit, den Knoten 40 zu entfernen, besteht darin, das linke Kind (35) nach oben zu verschieben und das rechte Kind (50) dort zu belassen, wo es war.

1
2
3
4
5

 30
/ \
15 35
\
50

Beide Möglichkeiten sind in Ordnung, solange man die Eigenschaft des binären Suchbaums beibehält: left < parent < right.

Löschen der Wurzel.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Das Löschen der Wurzel ist sehr ähnlich wie das bereits erwähnte Entfernen von Knoten mit 0, 1 oder 2 Kindern. Der einzige Unterschied ist, dass wir danach die Referenz der Wurzel des Baumes aktualisieren müssen.

Hier ist eine Animation dessen, was wir besprochen haben.

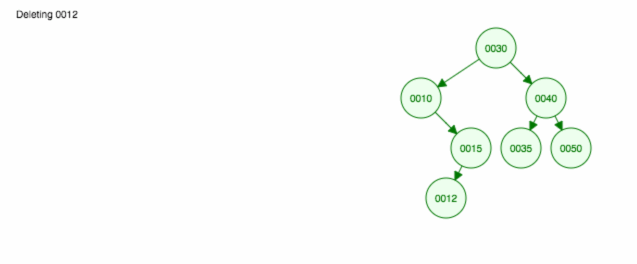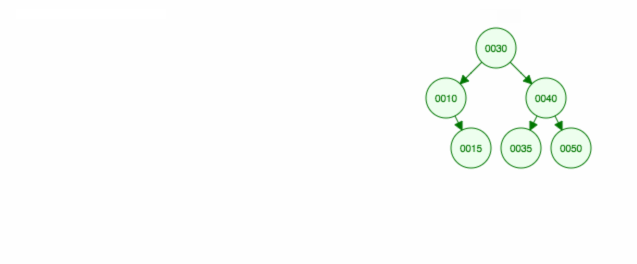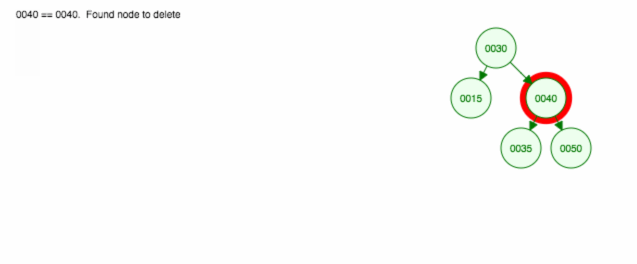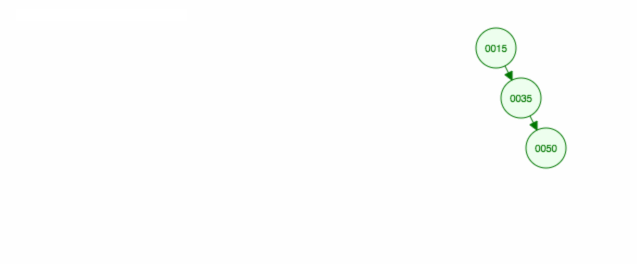
Die Animation bewegt das linke Kind/den linken Teilbaum nach oben und lässt das rechte Kind/den rechten Teilbaum an seinem Platz.

Nun, da wir eine gute Idee haben, wie es funktionieren sollte, lassen Sie uns es implementieren:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Hier sind einige Highlights der Implementierung:

• Zuerst suchen wir, ob der Knoten existiert. Wenn nicht, geben wir false zurück und sind fertig!
• Wenn der zu entfernende Knoten existiert, dann kombinieren wir linke und rechte Kinder zu einem Teilbaum.
• Ersetzen Sie den zu löschenden Knoten durch den kombinierten Teilbaum.

Die Funktion, die den linken in den rechten Teilbaum kombiniert, ist die folgende:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Sagen wir zum Beispiel, dass wir den folgenden Baum kombinieren wollen, und wir sind dabei, den Knoten 30 zu löschen. Wir wollen den linken Teilbaum von 30 in den rechten mischen. Das Ergebnis ist folgendes:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Wenn wir den neuen Teilbaum zur Wurzel machen, dann ist Knoten 30 nicht mehr da!

Binärbaum-Transversal

Es gibt verschiedene Möglichkeiten, einen Binärbaum zu durchlaufen, je nach der Reihenfolge, in der die Knoten besucht werden: in-order, pre-order und post-order. Wir können auch dieDFSundBFS verwenden, die wir in der Graph-Post gelernt haben.

In-Order-Traversal

In-Order-Traversal besucht Knoten in dieser Reihenfolge: links, parent, rechts.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Lassen Sie uns diesen Baum verwenden, um das Beispiel zu machen:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

Eine geordnete Traversierung würde die folgenden Werte ausgeben: 3, 4, 5, 10, 15, 30, 40. Wenn der Baum ein BST ist, dann werden die Knoten in aufsteigender Reihenfolge sortiert, wie in unserem Beispiel.

Post-Order Traversal

Post-Order Traversal besucht Knoten in dieser Reihenfolge: links, rechts, parent.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-Order Traversal würde die folgenden Werte ausgeben: 3, 4, 5, 15, 40, 30, 10.

Pre-Order-Traversal und DFS

Pre-Order-Traversal besucht Knoten in dieser Reihenfolge: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-Order-Traversal würde folgende Werte ausgeben: 10, 5, 4, 3, 30, 15, 40. Diese Reihenfolge der Zahlen ist das gleiche Ergebnis, das wir erhalten würden, wenn wir die Depth-First Search (DFS) ausführen würden.

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Wenn Sie eine Auffrischung zu DFS benötigen, haben wir es in Graph post ausführlich behandelt.

Breadth-First Search (BFS)

Ähnlich wie bei DFS können wir ein BFS implementieren, indem wir das Stack durch ein Queue ersetzen:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

Die BFS Reihenfolge ist: 10, 5, 30, 4, 15, 40, 3

Balanced vs. Non-balanced Trees

So weit haben wir besprochen, wie man add, remove und find Elemente. Wir haben jedoch noch nicht über die Laufzeiten gesprochen. Lassen Sie uns über den schlimmsten Fall nachdenken.

Angenommen, wir wollen Zahlen in aufsteigender Reihenfolge addieren.

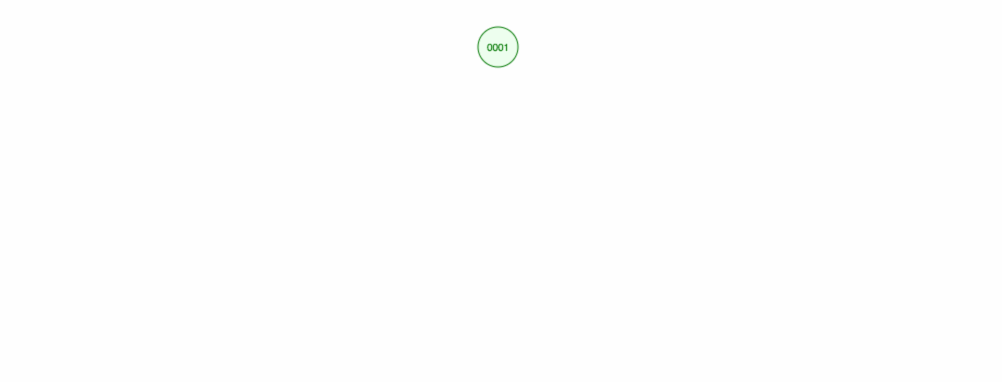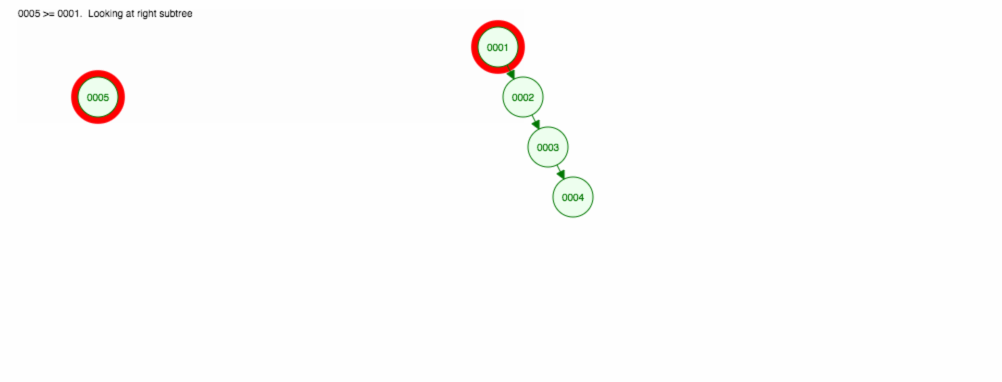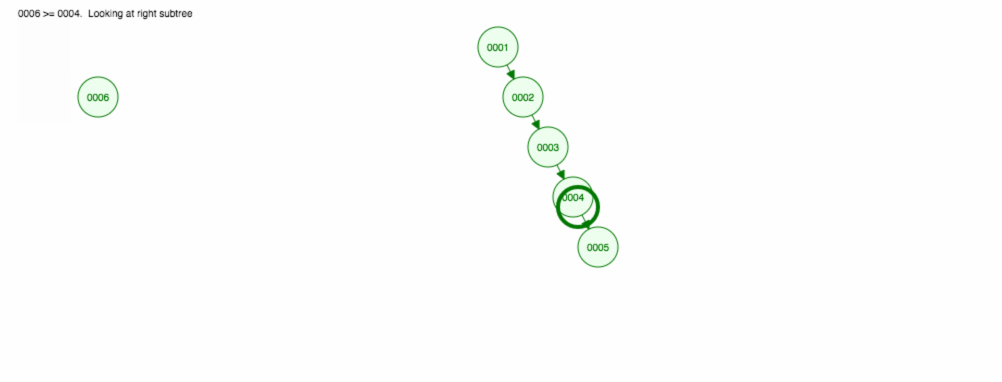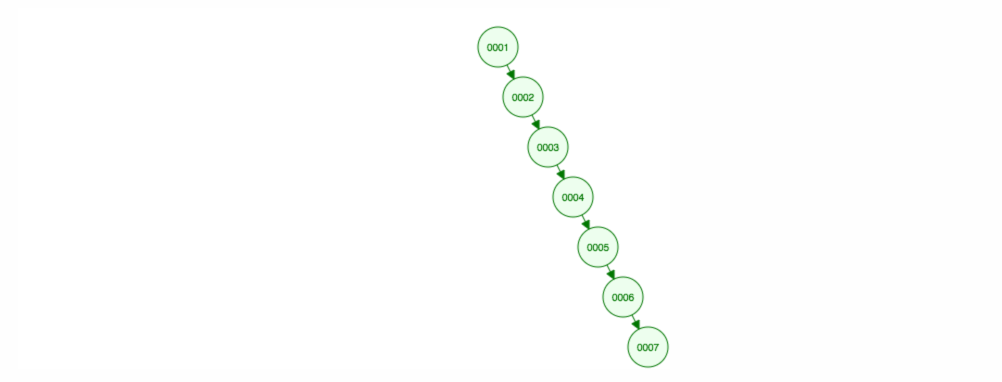
Am Ende befinden sich alle Knoten auf der rechten Seite! Dieser unausgewogene Baum ist nicht besser als eine LinkedList, so dass die Suche nach einem Element O(n) dauern würde. 😱

In einem unbalancierten Baum etwas zu suchen, ist so, als würde man ein Wort im Wörterbuch Seite für Seite suchen. Wenn der Baum balanciert ist, kann man das Wörterbuch in der Mitte öffnen, und von dort aus weiß man, ob man nach links oder rechts gehen muss, je nach Alphabet und dem Wort, das man sucht.

Wir müssen einen Weg finden, den Baum auszubalancieren!

Wenn der Baum balanciert wäre, könnten wir Elemente in O(log n) finden, anstatt jeden Knoten zu durchlaufen. Reden wir darüber, was ein ausgeglichener Baum bedeutet.

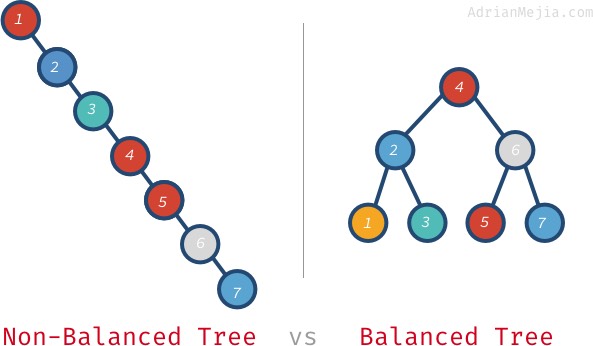
Wenn wir im nicht ausgeglichenen Baum nach 7 suchen, müssen wir von 1 bis 7 gehen. Im ausgeglichenen Baum besuchen wir jedoch: 4, 6, und 7. Bei größeren Bäumen wird es noch schlimmer. Wenn man eine Million Knoten hat, kann die Suche nach einem nicht existierenden Element bei einem ausgeglichenen Baum den Besuch aller Millionen Knoten erfordern. Es sind nur 20 Besuche nötig! Das ist ein riesiger Unterschied!

Wir werden dieses Problem im nächsten Beitrag mit selbstbalancierten Bäumen (AVL-Bäumen) lösen.

Zusammenfassung

Wir haben viel über Bäume gelernt. Fassen wir es in Stichpunkten zusammen:

• Der Baum ist eine Datenstruktur, bei der ein Knoten 0 oder mehr Nachkommen/Kinder hat.
• Baumknoten haben keine Zyklen (azyklisch). Wenn er Zyklen hat, ist er stattdessen eine Graph-Datenstruktur.
• Bäume mit zwei oder weniger Kindern werden genannt: Binärbaum
• Wenn ein Binärbaum so sortiert ist, dass der linke Wert kleiner als der des Elternteils und der rechte größer als der des Kindes ist, dann und nur dann haben wir einen Binärsuchbaum.
• Sie können einen Baum in einer Pre/Post/In-Order Weise besuchen.
• Ein Ungleichgewicht hat eine Zeitkomplexität von O(n). 🤦🏻
• Ein ausgeglichener hat eine Zeitkomplexität von O(log n). 🎉