Physikalische Chemie ist ein ziemlich breites Thema; es umfasst:

• Quantenchemie
• Thermochemie (Übersicht + Mehr)
• Kinetik (Übersicht + Mehr)
• Statistische Mechanik

Da es ziemlich viele Themen für eine Antwort gibt, werde ich nur zwei Beispiele pro Thema geben. Dies wird eine lange Antwort sein, aber Sie können sich auf das konzentrieren, wonach Sie suchen.

QUANTENCHEMIE

In der Quantenchemie geht es im Allgemeinen darum, Szenarien auf der pikroskopischen Skala zu verstehen, Systeme in geeigneten mathematischen Darstellungen zu modellieren und die entsprechenden Näherungen zu machen.

Zwei Beispiele für Quantenchemie sind:

• Einfacher harmonischer Oszillator (zwei Kugeln verbunden durch eine ideale Feder)

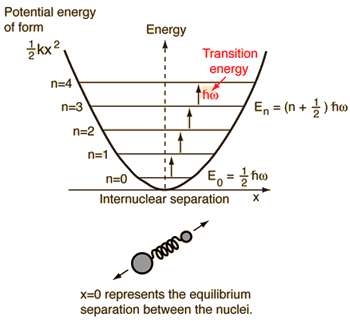
Für dieses System, das wir aus der Physik kennen, reduzieren wir es von einem klassischen Zweikörperproblem auf ein Einkörperproblem mit relativen Koordinaten und einer reduzierten Masse, #mu = (m_1m_2)/(m_1 + m_2)#.

Dieses System konzentriert sich auf das Verständnis der elastischen potentiellen Energie der Molekülbindung.

• Starrer Rotor (zwei Kugeln, die durch einen Stab verbunden sind, d.h. 100% steife Feder)

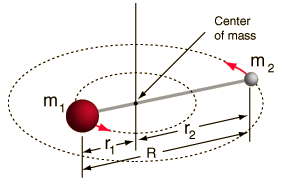
Dieses System ist eine Vereinfachung, da alle Moleküle eine Form von Bindungsstreckung/Schwingung haben (Sie würden verstehen, warum diese Vereinfachung in Ordnung ist, wenn Sie die Mathematik sehen würden!)

Allerdings erlaubt es uns, diese Winkelkomponente eines Zweikörpersystems zu zerlegen und die Rotationseigenschaften des Moleküls zu verstehen.

THERMOCHEMIE

Hier geht es um die makroskopische Skala von Wärmefluss, Arbeit, freien Energien usw. Das hat man in der allgemeinen Chemie schon einmal gemacht, und das wird wiederholt und erweitert.

Zwei Beispiele sind:

• Bestimmung thermodynamischer Werte aus messbaren Größen

Was ist Chemie, wenn sie nicht praktisch ist?

Ein gemeinsames Thema ist also die Fähigkeit, Ableitungen durchzuführen und die wichtigsten thermodynamischen Größen (Entropie, Enthalpie, freie Energie nach Gibbs und Helmholtz, innere Energie) in Form von natürlichen Größen wie Volumen, Temperatur und Druck auszudrücken.

Zum Beispiel kann man die Entropie aus einer isothermen Expansion (#DeltaT = 0, DeltaV > 0#) berechnen, wenn man #V_2# und #V_1# oder #P_2# und #P_1# kennt, und zwar für ein einatomiges ideales Gas:

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Ideale und nichtideale Nicht-Elektrolyt/Elektrolyt-Lösungen

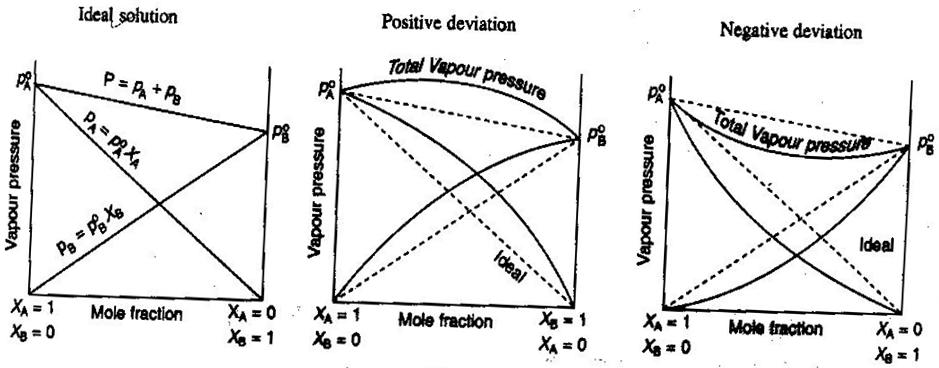
In der allgemeinen Chemie, behandeln wir Lösungen gerne ideal, so dass Volumina additiv sind, Konzentrationen von starken Elektrolyten gerade #“mol/L „#-Berechnungen sind und so weiter. Einige Möglichkeiten, wie Lösungen nicht ideal sein können:

• Die Lösung kann sich nach dem Mischen ausdehnen oder zusammenziehen.
• Die Ionenpaarung verringert die Ionenstärke der Lösung und reduziert den van’t Hoff-Faktor #i# des gelösten Stoffes.
• Die Entweichungstendenz des gelösten Stoffes verändert seine effektive Konzentration (seine Aktivität).

KINETIK

Das haben Sie vielleicht schon einmal in einem allgemeinen Chemieunterricht oder vielleicht in der High School gemacht. Die Physikalische Chemie geht etwas weiter, indem sie die Reaktionsmechanismen und die Gasphasendynamik genauer betrachtet.

Zwei Beispiele:

• Näherung des stationären Zustands

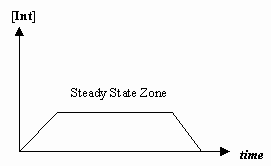
Manchmal ist die Geschwindigkeit des ersten mechanischen Schritts viel langsamer als die des zweiten Schritts, und wir nähern uns an, dass sich die Konzentration des Zwischenprodukts tatsächlich nicht ändert (#(d)/(dt) = 0#).

Damit lässt sich ein für einen Mechanismus spezifisches Geschwindigkeitsgesetz ableiten, und wir können eine „beobachtete Geschwindigkeitskonstante“ in Form der Geschwindigkeitskonstanten für die einzelnen Schritte ausdrücken.

• Reale Gasgesetze

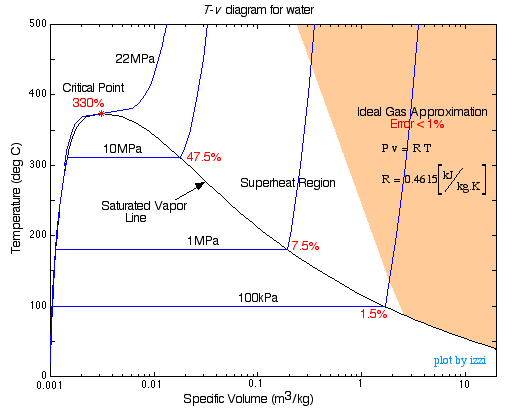
Die van-der-Waals-Zustandsgleichung haben Sie vielleicht schon kennengelernt:

#(V – nb) = nRT#

Nun, es gibt noch einige andere, wie die Redlich-Kwong, die Peng-Robinson, und so weiter.

Die Grundidee ist, dass sie alle für bestimmte Gase besser funktionieren als für andere, aber sie funktionieren alle, um die realen Eigenschaften von Gasen zu berücksichtigen, anstatt anzunehmen, dass alle eine elastisch kollidierende träge Punktmasse sind.

STATISTISCHE MECHANIK

Mit der statistischen Mechanik gehen wir einen Schritt zurück und betrachten die pikroskopische Welt aus einer makroskopischen Perspektive:

„Was können wir von einem System lernen, wenn wir wie ein Quantenchemiker über eine große Ansammlung von Teilchen nachdenken?“

Zwei Beispiele:

• Equipartitionstheorem

#<< K >> = N/2nRT = N/2 k_BT#,

wobei #N# die Anzahl der Freiheitsgrade für jede Art von Bewegung (linear, rotierend, schwingend, elektronisch, nuklear) ist. Im Grunde genommen wird jede Bewegungsart in einem Molekül berücksichtigt, um seine durchschnittliche kinetische Energie, #<< K >>#, zu schätzen.

Dies funktioniert nur bei „ausreichend hohen“ Temperaturen. Normalerweise ist es für Translations- und Rotationsbewegungen in Ordnung, aber es neigt dazu, die Beiträge von Schwingungen zu überschätzen.

• Die mikrokanonische Teilungsfunktion

#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)#,

wobei:

• #g_i# die Entartung des Zustands #i# mit der Energie #epsilon_i# ist.
• #N# ist die Gesamtzahl der verfügbaren Zustände.

Genauso wie die Wellenfunktion #psi# alles über ein quantenmechanisches System aussagt, gibt die mikrokanonische Partitionsfunktion an, wie ein Molekül seine verfügbare Energie auf die möglichen Zustandsarten (Translations-, Rotations-, Vibrations-, Elektronen- und Kernzustand) verteilen kann.

Für jede Zustandsart gibt es ein #q#: #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)# und #q_(n uc)#.

Aus der Kenntnis jeder Art von #q# lassen sich die bekannten thermodynamischen Größen wie Entropie (#S#), Enthalpie (#H#), Gibbs’sche freie Energie (#G#) usw. in Form jeder Art von #q# ableiten.

Als nützliches Beispiel kann die absolute molekulare Entropie bei JEDER Temperatur in den meisten Fällen berechnet werden als:

#S/N = k_B ln (q/N)_“tot“ + (<< epsilon >>_“tot“)/T + k_B#,

wobei:

• #k_B ~~ „0.695 cm“^(-1)“/K „# ist die Boltzmann-Konstante.
• #(q/N)_“tot“ = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# ist die gesamte mikrokanonische Verteilungsfunktion, die alle möglichen Arten von Zuständen umfasst, und #N# ist die Gesamtzahl der betrachteten Moleküle.
• #<< epsilon >> = E/N# ist die Molekularenergie, definiert als #<< epsilon >> = k_BT^2((del ln (q“/“N)_“tot“)/(del T))_V#.

(Ja, mit dieser Formel kann man bei #“298,15 K „# das gleiche #S^@# berechnen, das man im Anhang des Lehrbuchs sieht!)

Ein Beispiel für die Anwendung dieser Formel findet sich hier.