Fysikaalinen kemia on jokseenkin laaja aihe; se kattaa:

• Kvanttikemia
• Lämpökemia (kertausta + lisää)
• Kinetiikka (kertausta + lisää)
• Statistinen mekaniikka

Koska aiheita on melko paljon yhteen vastaukseen, annan vain kaksi esimerkkiä per aihe. Tästä tulee pitkä vastaus, mutta voit keskittyä siihen, mitä etsit.

KVANTUMIKEMIA

Kvantumikemiassa on yleensä kyse siitä, että yritetään ymmärtää skenaarioita mikroskooppisessa mittakaavassa, mallinnetaan systeemejä sopivilla matemaattisilla esityksillä ja tehdään sopivia approksimaatioita.

Kaksi esimerkkiä kvanttikemiasta ovat:

• Yksinkertainen harmoninen oskillaattori (kaksi palloa, jotka on liitetty toisiinsa ideaalijousella)

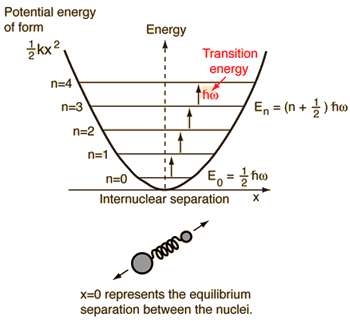
Tälle systeemille, jonka tunnemme fysiikasta, redusoimme sen klassisesta kahden kappaleen ongelmasta yhden kappaleen ongelmaksi, jossa on suhteelliset koordinaatit ja pelkistetty massa, #mu = (m_1m_2)/(m_1 + m_2)#.

Tässä järjestelmässä keskitytään molekyylisidoksen elastisen potentiaalienergian ymmärtämiseen.

• Jäykkä roottori (kaksi palloa, jotka on yhdistetty sauvalla, eli 100 % jäykkä jousi)

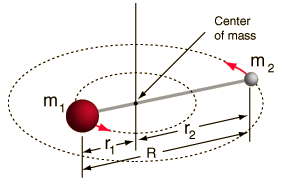
Tämä systeemi on yksinkertaistus, sillä kaikissa molekyyleissä on jonkinlaista sidoksen venymistä/värähtelyä (ymmärtäisit, miksi tämä yksinkertaistus on OK, jos näkisit matematiikan!).

Mutta sen avulla voimme purkaa tämän kahden kappaleen systeemin kulmakomponentin ja ymmärtää molekyylin rotaatio-ominaisuuksia.

THERMOKEMIA

Tässä tarkastellaan makroskooppisella mittakaavalla lämpövirtaa, työtä, vapaita energioita ja niin edelleen.

Yhteinen teema on siis pystyä suorittamaan derivaattoja ja ilmaisemaan tärkeimmät termodynaamiset suureet (entropia, entalpia, Gibbs + Helmholtzin vapaa energia, sisäenergia) luonnollisten muuttujien, kuten tilavuuden, lämpötilan ja paineen, avulla.

Voidaan esimerkiksi laskea entropia isotermisestä paisumisesta (#DeltaT = 0, DeltaV > 0#) tietämällä #V_2# ja #V_1# tai #P_2# ja #P_1#, ja tämä yksiatomiselle ideaalikaasulle:

#DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1) = nRln(V_2/V_1)#

• Ideaaliset ja ei-ideaaliset ei-elektrolyytit/elektrolyyttiliuokset

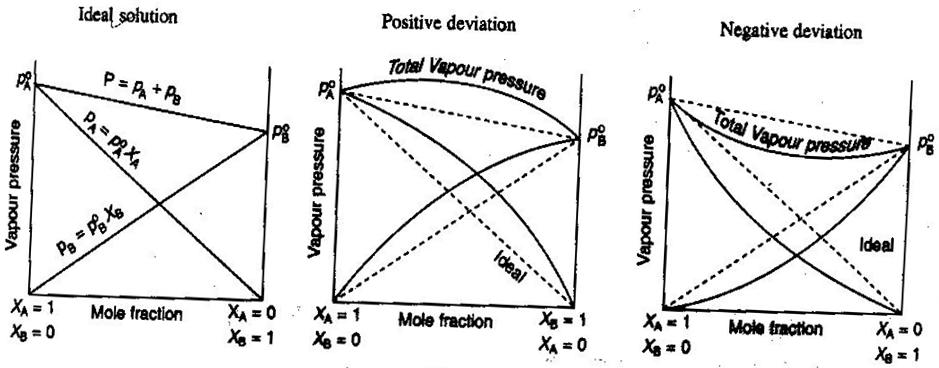
Yleisessä kemiassa, haluamme käsitellä liuoksia ideaalisesti, niin että tilavuudet ovat additiivisia, vahvojen elektrolyyttien konsentraatiot ovat suoria #”mol/L ”# -laskelmia ja niin edelleen. Joitakin tapoja, joilla liuokset eivät ole ihanteellisia:

• Liuos voi laajentua tai supistua sekoittamisen jälkeen.
• Ionien pariutuminen vähentää liuoksen ionivahvuutta ja pienentää liuenneen aineen van’t Hoffin kerrointa #i#.
• Liuenneen aineen karkaamistaipumus muuttaa sen tehollista konsentraatiota (aktiivisuutta).

KINETIIKKA

Olet ehkä tehnyt tätä ennenkin yleisellä kemian tunnilla tai ehkä lukiossa. Fysikaalinen kemia laajentaa tätä hieman enemmän tarkastelemalla tarkemmin reaktiomekanismeja ja kaasufaasin dynamiikkaa.

Kaksi esimerkkiä:

• Tasaisen tilan approksimaatio

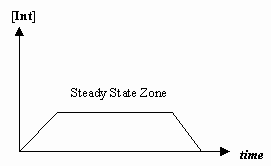
Joskus ensimmäisen mekanistisen vaiheen nopeus on paljon hitaampi kuin toisen vaiheen nopeus, ja approksimoimme, että välituotteen konsentraatio ei tosiasiassa muutu (#(d)/(dt) = 0#).

Tällöin voidaan johtaa mekanismille ominainen nopeuslaki ja ilmaista ”havaittu nopeusvakio” yksittäisten vaiheiden nopeusvakioiden avulla.

• Reaaliset kaasulait

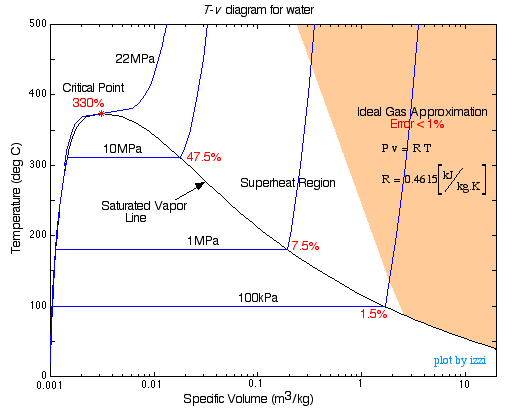
Olet ehkä tutustunut van der Waalsin tilanyhtälöön:

#(V – nb) = nRT#

Nyt on muitakin, kuten Redlichin-Kwongin, Peng-Robinsonin ja niin edelleen.

Perusajatuksena on, että ne kaikki toimivat paremmin tietyille kaasuille kuin toisille, mutta ne kaikki toimivat kaasujen todellisten ominaisuuksien huomioon ottamiseksi sen sijaan, että oletettaisiin kaikkien olevan elastisesti törmäileviä inerttejä pistemassoja.

STATISTINEN MEKANIIKKA

Tilastollisessa mekaniikassa otamme askeleen taaksepäin ja tarkastelemme mikroskooppista maailmaa makroskooppisesta näkökulmasta:

”Mitä voimme oppia systeemistä, jos ajattelemme kvanttikemistin tavoin suuresta hiukkaskokoelmasta?”

Kaksi esimerkkiä:

• Equipartition Theorem

#<< K >> = N/2nRT = N/2 k_BT#,

joissa #N# on kunkin liiketyypin (lineaarinen, rotaatio-, värähdys-, elektroninen-, ydinvoima-, ydinvoima-) vapausasteiden lukumäärä. Periaatteessa se ottaa huomioon molekyylin jokaisen liiketyypin arvioidakseen sen keskimääräisen liike-energian, #<< K >>#.

Tämä toimii vain ”riittävän korkeissa” lämpötiloissa. Yleensä se on OK translaatio- ja rotaatioliikkeille, mutta sillä on taipumus yliarvioida värähtelyosuudet.

• Mikrokanoninen jakautumisfunktio

#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)#,

joissa:

• #g_i# on tilan #i# rappeutuneisuus, jolla on energia #epsilon_i#.
• #N# on käytettävissä olevien tilojen kokonaismäärä.

Aivan kuten aaltofunktio #psi# määrittelee kaiken kvanttimekaanisesta systeemistä, mikrokanoninen partitiofunktio määrittelee, miten molekyyli voi jakaa käytettävissä olevan energiansa mahdollisiin tilatyyppeihin (translaatio-, rotaatio-, värähtely-, elektroniikka- ja ydintilatyyppeihin).

Kullekin tilatyypille on olemassa #q#: #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)# ja #q_(n uc)#.

Kunkin #q#-tyypin tuntemisesta voidaan johtaa tutut termodynaamiset suureet, kuten entropia (#S#), entalpia (#H#), Gibbsin vapaa energia (#G#) ja niin edelleen, kunkin #q#-tyypin suhteen.

Hyödyllisenä esimerkkinä absoluuttinen molekyylientropia MISSÄ tahansa lämpötilassa voidaan useimmissa tapauksissa laskea seuraavasti:

#S/N = k_B ln (q/N)_”tot” + (<< epsilon >>_”tot”)/T + k_B#,

missä:

• #k_B ~~”0.695 cm”^(-1)”/K ”# on Boltzmannin vakio.
• #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# on kokonaismikrokanoninen jakautumisfunktio, joka sisältää kaikki mahdolliset tilatyypit, ja #N# on tarkasteltujen molekyylien kokonaismäärä.
• #<< epsilon >> = E/N# on molekyylien energia, joka määritellään kaavalla #<< epsilon >> = k_BT^2((del ln (q”/”N)_”tot”)/(del T))_V#.

(Kyllä, tämän kaavan avulla #”298,15 K ”# lämpötilassa voidaan laskea sama #S^@# kuin oppikirjan liitteessä!)

Esimerkki tästä kaavasta käytössä löytyy täältä.