A fa adatszerkezeteket sokféleképpen használhatjuk, és nem árt, ha tisztában vagyunk a működésükkel. A fák képezik az alapját más, igen gyakran használt adatszerkezeteknek, mint például a Térképek és a Halmazok. Emellett adatbázisokban is használják őket gyors keresések elvégzésére. A HTML DOM fa adatszerkezetet használ az elemek hierarchiájának ábrázolására. Ebben a bejegyzésben a fák különböző típusait, például a bináris fákat, a bináris keresőfákat és ezek megvalósítását fogjuk megvizsgálni.

Az előző bejegyzésben a gráf adatszerkezeteket vizsgáltuk, amelyek a fák egy általánosított esete. Kezdjük el megtanulni, hogy mik is azok a fa adatszerkezetek!

Ez a bejegyzés egy oktatósorozat része:

Adatstruktúrák és algoritmusok (DSA) tanulása kezdőknek

1. Előadás az algoritmusok időbonyolultságáról és a Big O jelölésről

2. Nyolc időbonyolultság, amit minden programozónak tudnia kell

3. Adatstruktúrák kezdőknek:

4. Gráf adatszerkezetek kezdőknek

5. Fák adatszerkezetek kezdőknek 👈 you are here

6. Self-balanced Binary Search Trees

7. Appendix I: Rekurzív algoritmusok elemzése

Fák: alapfogalmak

A fa olyan adatszerkezet, ahol egy csomópontnak nulla vagy több gyermeke lehet. Minden csomópont tartalmaz egy értéket. A gráfokhoz hasonlóan a csomópontok közötti kapcsolatot éleknek nevezzük. A fa a gráfok egy típusa, de nem minden gráf fa (erről később).

Az ilyen adatszerkezeteket azért nevezzük “fának”, mert az adatszerkezet hasonlít egy fára 🌳. Egy gyökércsomóponttal kezdődik, és annak leszármazottaival ágazik el, végül pedig vannak levelek.

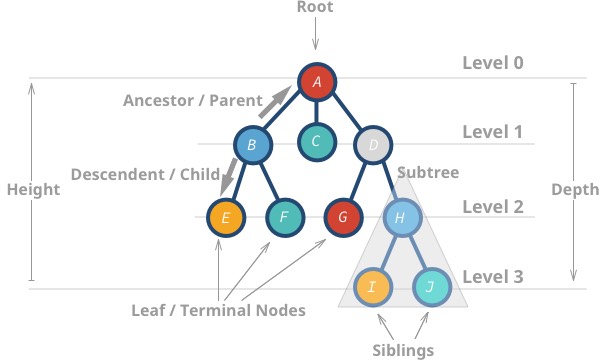
Itt van a fák néhány tulajdonsága:

• A legfelső csomópontot gyökérnek nevezzük.
• A gyermek nélküli csomópontot levélcsomópontnak vagy végcsomópontnak nevezzük.
• A fa magassága (h) a legtávolabbi levél és a gyökér közötti távolság (élszám).
  • A magassága 3
  • I magassága 0
• Egy csomópont mélysége vagy szintje a gyökér és az adott csomópont közötti távolság.
  • H mélysége 2
  • B mélysége 1

Egy egyszerű fa adatszerkezet megvalósítása

Amint korábban láttuk, egy facsomópont csak egy adatszerkezet egy értékkel és a leszármazottakra mutató linkekkel.

Itt egy példa egy facsomópontra:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Egy fát 3 leszármazottal a következőképpen hozhatunk létre:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Ez minden; van egy fa adatszerkezetünk!

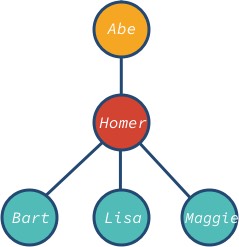
A abe csomópont a gyökér, bart, lisa és maggie pedig a fa levélcsomópontjai. Vegyük észre, hogy a fa csomópontjának különböző leszármazottai lehetnek: 0, 1, 3 vagy bármilyen más érték.

A fa adatszerkezeteknek számos alkalmazása van, például:

• Térképek
• Készletek
• Adatbázisok
• Priority Queues
• Kérdezés egy LDAP (Lightweight Directory Access Protocol)
• A dokumentum objektum modell (DOM) megjelenítése a HTML számára a webhelyeken.

Bináris fák

A fák csomópontjainak nulla vagy több gyermeke lehet. Ha azonban egy fának legfeljebb két gyermeke van, akkor bináris fának nevezzük.

Teljes, teljes és tökéletes bináris fák

Attól függően, hogy a csomópontok hogyan helyezkednek el egy bináris fában, az lehet teljes, teljes és tökéletes:

• Teljes bináris fa: minden csomópontnak pontosan 0 vagy 2 gyermeke van (de soha nem 1).
• Teljes bináris fa: amikor az utolsó kivételével minden szint tele van csomóponttal.
• Tökéletes bináris fa: amikor minden szint (beleértve az utolsót is) tele van csomóponttal.

Nézd meg ezeket a példákat:

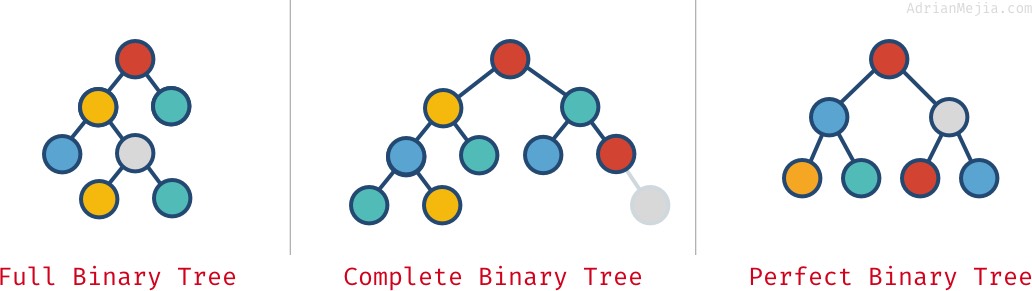
Ezek a tulajdonságok nem mindig zárják ki egymást. Több is lehet:

• A tökéletes fa mindig teljes és teljes.
  • A tökéletes bináris fáknak pontosan `2^k – 1` csomópontja van, ahol k a fa utolsó szintje (1-gyel kezdődik).
• A teljes fa nem mindig full.
  • Mint a “teljes” példánkban, hiszen van olyan szülő, amelynek csak egy gyermeke van. Ha a jobb szélső szürke csomópontot eltávolítjuk, akkor egy teljes és teljes fát kapunk, de nem tökéleteset.
• A teljes fa nem mindig teljes és tökéletes.

Bináris keresőfa (BST)

A bináris keresőfák vagy röviden BST a bináris fák egy speciális alkalmazása. A BST legfeljebb két csomóponttal rendelkezik (mint minden bináris fa). Az értékek azonban úgy vannak megadva, hogy a bal oldali gyermek értéke kisebb legyen, mint a szülőé, a jobb oldali gyermeké pedig nagyobb.

Duplikátumok: Néhány BST nem engedi a duplikátumokat, míg mások ugyanazokat az értékeket adják hozzá jobboldali gyermekként. Más implementációk számon tarthatják a duplikáció esetét (ezzel később foglalkozunk).

Implementáljunk egy bináris keresőfát!

BST implementáció

A BST nagyon hasonlít a korábbi fa implementációnkhoz. Van azonban néhány különbség:

• A csomópontoknak legfeljebb csak két gyermekük lehet: bal és jobb oldali.
• A csomópontok értékeit left < parent < right módon kell rendezni.

Itt van a fa csomópontja. Nagyon hasonló a korábbiakhoz, de hozzáadtunk néhány praktikus gettert és settert a bal és jobb gyerekeknek. Vegyük észre, hogy a szülőre is tart egy hivatkozást, és ezt frissítjük minden alkalommal, amikor gyerekeket adunk hozzá.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Oké, eddig tudunk bal és jobb gyereket hozzáadni. Most pedig csináljuk meg a BST osztályt, amely érvényesíti a left < parent < right szabályt.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Végrehajtjuk a beszúrást.

BST csomópont beszúrása

Hogy beszúrjunk egy csomópontot egy bináris fába, a következőket tesszük:

1. Ha a fa üres, az első csomópont lesz a gyökér, és kész.
2. Hasonlítsuk össze a gyökér/szülő értékét, ha magasabb, menjünk jobbra, ha alacsonyabb, menjünk balra. Ha ugyanaz, akkor az érték már létezik, így növelhetjük a duplikátumok számát (multiplicity).
3. Mondjuk újra a #2-t, amíg nem találunk egy üres helyet az új csomópont beillesztéséhez.

Mutatunk egy illusztrációt, hogyan illesszük be a 30, 40, 10, 15, 12, 50 értékeket:

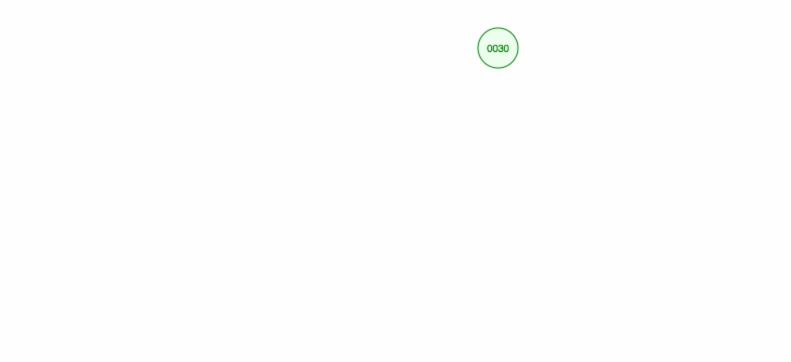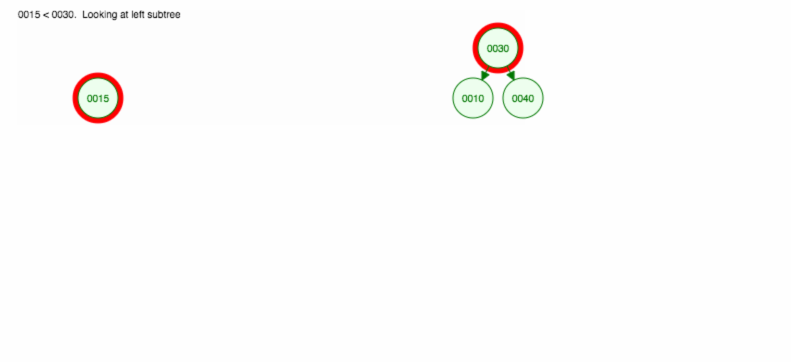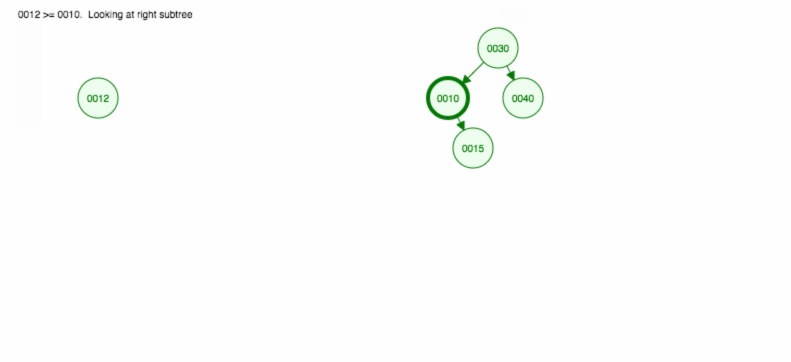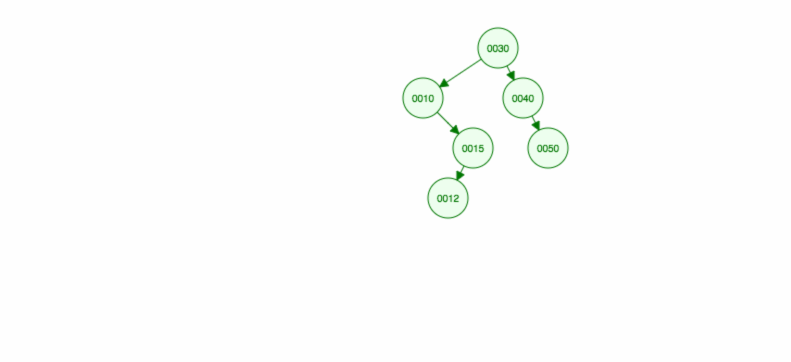
A beszúrást a következőképpen valósíthatjuk meg:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Egy findNodeAndParent nevű segédfüggvényt használunk. Ha úgy találjuk, hogy a csomópont már létezik a fában, akkor növeljük a multiplicity számlálót. Lássuk, hogyan valósul meg ez a függvény:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent végigmegy a fán, keresve az értéket. A gyökérnél kezd (2. sor), majd az érték alapján balra vagy jobbra halad (10. sor). Ha az érték már létezik, akkor visszaadja a found csomópontot és a szülőt is. Abban az esetben, ha a csomópont nem létezik, akkor is visszaadja a parent.

BST csomópont törlése

Tudjuk, hogyan kell értéket beszúrni és keresni. Most a törlési műveletet fogjuk megvalósítani. Ez egy kicsit trükkösebb, mint a hozzáadás, ezért a következő esetekkel magyarázzuk el:

Levél csomópont törlése (0 gyermek)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Eltávolítjuk a csomópont szülőjének (15) hivatkozását, hogy null legyen.

Egy gyermekes csomópont törlése.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

Ez esetben a szülőhöz (30) megyünk, és a gyermek (10) helyébe egy gyermek gyermekét (15) tesszük.

Két gyermekkel rendelkező csomópont törlése

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Eltávolítjuk a 40-es csomópontot, amelynek két gyermeke van (35 és 50). A szülő (30) gyermekét (40) kicseréljük a szülő jobb oldali gyermekére (50). Ezután a bal oldali gyermeket (35) ugyanott tartjuk, ahol korábban, tehát az 50 bal oldali gyermekévé kell tennünk.

A 40-es csomópont eltávolításának másik módja, hogy a bal oldali gyermeket (35) feljebb helyezzük, majd a jobb oldali gyermeket (50) ott tartjuk, ahol volt.

1
2
3
4
5

 30
/ \
15 35
\
50

Egyik mód is rendben van, amíg megtartjuk a bináris keresőfa tulajdonságát: left < parent < right.

A gyökér törlése.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

A gyökér törlése nagyon hasonló a korábban tárgyalt 0, 1 vagy 2 gyermekes csomópontok eltávolításához. Az egyetlen különbség, hogy utána frissítenünk kell a fa gyökerének hivatkozását.

Itt egy animáció a megbeszéltekről.

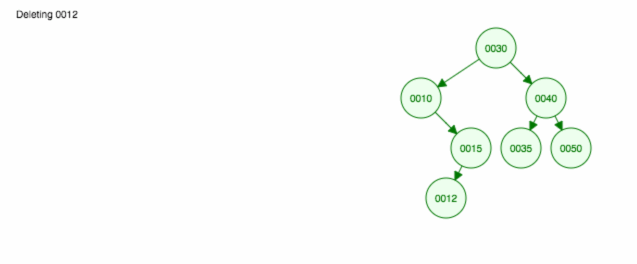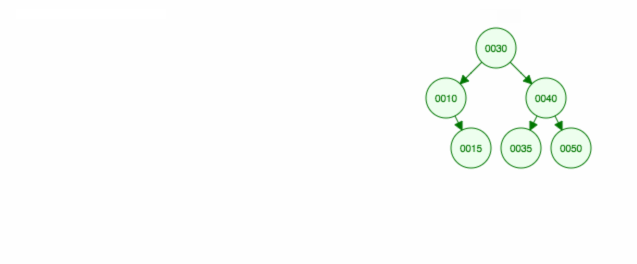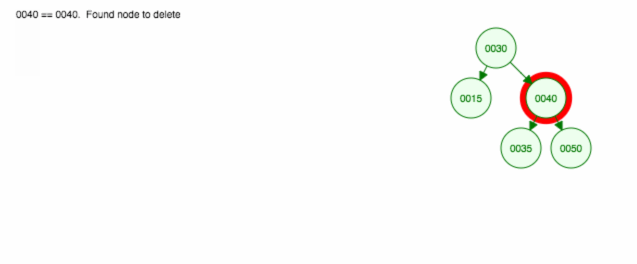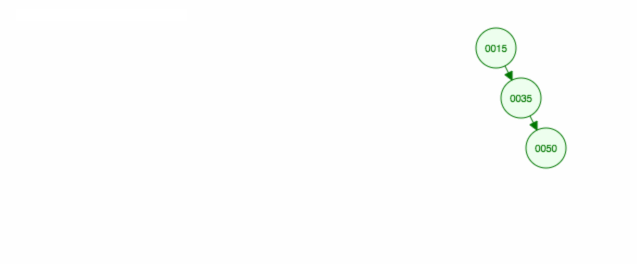
Az animáció felfelé mozgatja a bal oldali gyermeket/alfát, a jobb oldali gyermeket/alfát pedig a helyén tartja.

Most, hogy már tudjuk, hogyan kell működnie, valósítsuk meg:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Itt van az implementáció néhány fontosabb részlete:

• Először is megkeressük, hogy létezik-e a csomópont. Ha nem létezik, akkor false-t adunk vissza, és kész!
• Ha az eltávolítandó csomópont létezik, akkor a bal és jobb oldali gyermekeket egyesítjük egy részfává.
• A törlendő csomópontot az egyesített részfával helyettesítjük.

A bal oldali és jobb oldali részfát egyesítő függvény a következő:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Tegyük fel például, hogy a következő fát szeretnénk kombinálni, és a 30 csomópontot akarjuk törölni. A 30-as bal oldali részfát szeretnénk a jobb oldali részfába keverni. Az eredmény a következő:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Ha az új részfát tesszük gyökérré, akkor a 30 csomópont megszűnik!

Bináris fa átszelése

Egy bináris fa átszelésének különböző módjai vannak, attól függően, hogy a csomópontokat milyen sorrendben látogatjuk meg: sorrendben, sorrend előtt és sorrend után. Emellett használhatjuk őketDFSésBFSamit agraph post-ban tanultunk.Menjünk végig mindegyiken.

In-order Traversal

In-order traversal visit nodes on this order: left, parent, right.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Használjuk ezt a fát a példa elkészítéséhez:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

A sorrendben történő átsorolás a következő értékeket írná ki: 3, 4, 5, 10, 15, 30, 40. Ha a fa egy BST, akkor a csomópontok felmenő sorrendben lesznek rendezve, mint példánkban.

Sorrend utáni traverzálás

A rend utáni traverzálás a következő sorrendben látogatja meg a csomópontokat: balra, jobbra, szülő.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

A post-order traversal a következő értékeket írná ki: 3, 4, 5, 15, 40, 30, 10.

Sorrend előtti keresztezés és DFS

Sorrend előtti keresztezés a csomópontokat ebben a sorrendben látogatja meg: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

A preorder traversal a következő értékeket írná ki: 10, 5, 4, 3, 30, 15, 40. Ez a számsorrend ugyanaz az eredmény, mint amit a Depth-First Search (DFS) futtatása esetén kapnánk.

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Ha felfrissítésre van szüksége a DFS-ről, részletesen foglalkoztunk vele a Graph postban.

Breadth-First Search (BFS)

A DFS-hez hasonlóan egy BFS-t is megvalósíthatunk úgy, hogy a Stack-t egy Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

A BFS sorrendje a következő: 10, 5, 30, 4, 15, 40, 3

Kiegyensúlyozott vs. nem kiegyensúlyozott fák

Az eddigiekben a add, remove és find elemeket tárgyaltuk. Nem beszéltünk azonban a futási időkről. Gondoljunk a legrosszabb esetekre.

Tegyük fel, hogy a számokat növekvő sorrendben akarjuk összeadni.

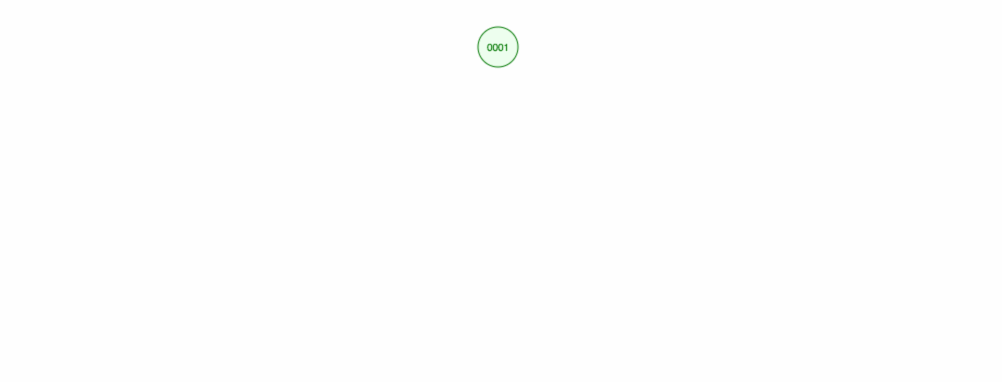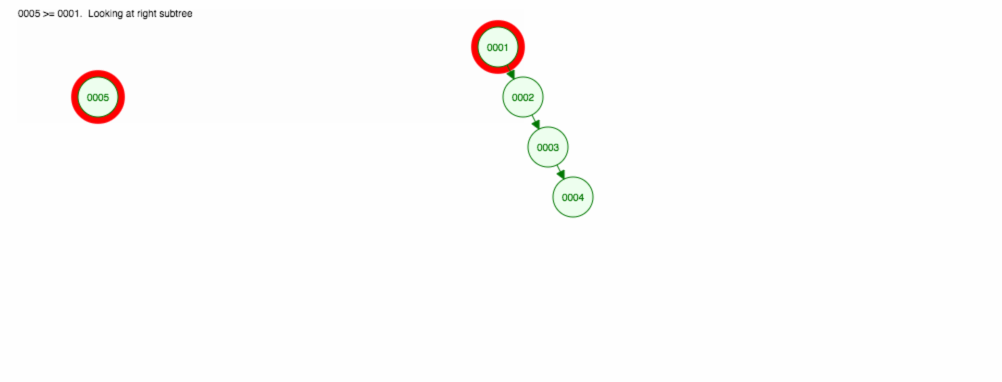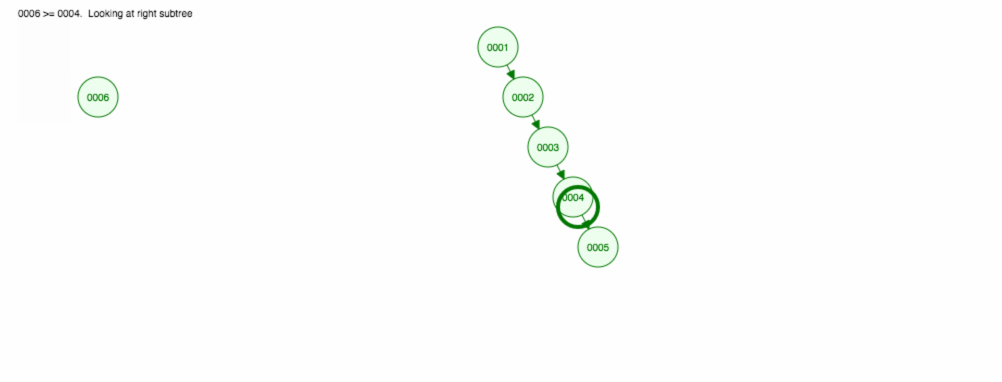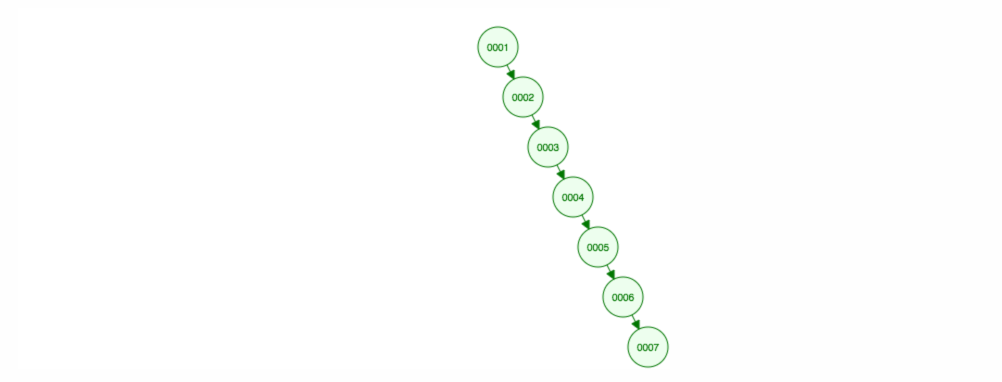
A végén az összes csomópont a jobb oldalon lesz! Ez a kiegyensúlyozatlan fa nem jobb, mint egy LinkedList, így egy elem megtalálása O(n) időt vesz igénybe. 😱

Egy kiegyensúlyozatlan fában keresni valamit olyan, mintha a szótárban oldalanként keresnénk egy szót. Ha a fa kiegyensúlyozott, akkor a szótárat középen kinyithatjuk, és onnan tudjuk, hogy az ábécétől és a keresett szótól függően balra vagy jobbra kell-e mennünk.

Meg kell találnunk a fa kiegyensúlyozásának módját!

Ha a fa kiegyensúlyozott lenne, akkor O(log n) alatt találhatnánk elemeket ahelyett, hogy minden egyes csomóponton végigmennénk. Beszéljünk arról, hogy mit jelent a kiegyensúlyozott fa.

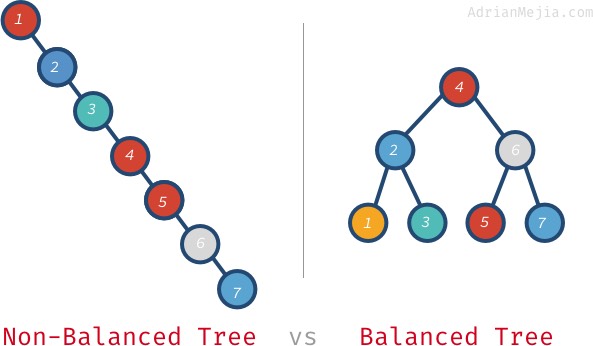
Ha a nem kiegyensúlyozott fában keressük 7, akkor 1-től 7-ig kell mennünk. A kiegyensúlyozott fában azonban meglátogatjuk: 4, 6 és 7. Nagyobb fáknál ez még rosszabb lesz. Ha egymillió csomópontunk van, egy nem létező elem kereséséhez a kiegyensúlyozott fán mind az egymilliót meg kell látogatnunk. Csak 20 látogatásra van szükség! Ez óriási különbség!

A következő bejegyzésben ezt a problémát fogjuk megoldani az önegyensúlyozott fák (AVL fák) használatával.

Összegzés

A fák esetében sok mindent lefedtünk. Foglaljuk össze gömbölyűen:

• A fa egy olyan adatszerkezet, ahol egy csomópontnak 0 vagy több leszármazottja/gyermeke van.
• A fa csomópontjainak nincsenek ciklusai (aciklikus). Ha vannak ciklusai, akkor helyette Graph adatstruktúra.
• A két vagy kevesebb gyermekkel rendelkező fák az ún: Bináris fa
• Ha egy bináris fát úgy rendezünk, hogy a bal oldali értéke kisebb, mint a szülőé, a jobb oldali gyermeké pedig nagyobb, akkor és csak akkor van bináris keresőfánk.
• Egy fát meglátogathatunk pre/post/in-order módon.
• Egy kiegyensúlyozatlan fa időbonyolultsága O(n). 🤦🏻
• A kiegyensúlyozottnak O(log n) az időbonyolultsága. 🎉