Tree data structuren worden veel gebruikt, en het is goed om een basis begrip te hebben van hoe ze werken. Bomen zijn de basis voor andere veelgebruikte datastructuren zoals Maps en Sets. Ze worden ook gebruikt in databases om snelle zoekacties uit te voeren. De HTML DOM gebruikt een boomstructuur om de hiërarchie van elementen weer te geven. Deze post zal de verschillende soorten bomen onderzoeken, zoals binaire bomen, binaire zoekbomen, en hoe ze te implementeren.

We hebben in de vorige post grafische gegevensstructuren onderzocht, die een gegeneraliseerd geval van bomen zijn. Laten we beginnen te leren wat boom-gegevensstructuren zijn!

Dit bericht maakt deel uit van een tutorial-serie:

Leren van Data Structuren en Algoritmen (DSA) voor Beginners

1. Intro in de tijdcomplexiteit van algoritmen en Big O notatie

2. Acht tijdcomplexiteiten die iedere programmeur zou moeten weten

3. Data Structuren voor Beginners: Arrays, HashMaps, en Lists

4. Graph Data Structures for Beginners

5. Trees Data Structures for Beginners 👈 u bent hier

6. Zelfgebalanceerde Binaire Zoekbomen

7. Aanhangsel I: Analyse van recursieve algoritmen

Bomen: basisbegrippen

Een boom is een gegevensstructuur waarin een knooppunt nul of meer kinderen kan hebben. Elk knooppunt bevat een waarde. Net als bij grafieken worden de verbindingen tussen knooppunten randen genoemd. Een boom is een soort grafiek, maar niet alle grafieken zijn bomen (daarover later meer).

Deze gegevensstructuren worden “bomen” genoemd omdat de gegevensstructuur op een boom lijkt 🌳. Het begint met een wortelknooppunt en vertakt zich met zijn afstammelingen, en ten slotte zijn er bladeren.

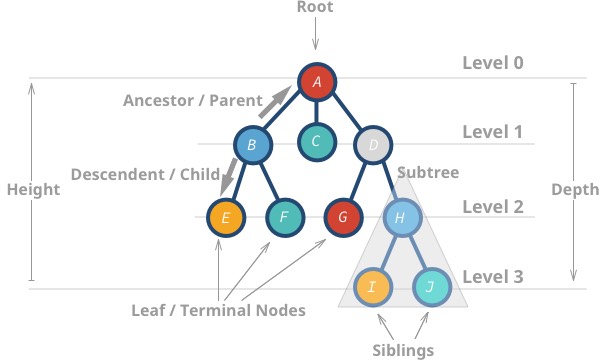
Hier zijn enkele eigenschappen van bomen:

• Het bovenste knooppunt wordt wortel genoemd.
• Een knooppunt zonder kinderen wordt bladknooppunt of eindknooppunt genoemd.
• De hoogte (h) van de boom is de afstand (aantal ribben) tussen het verste blad en de wortel.
  • A heeft een hoogte van 3
  • I heeft een hoogte van 0
• De diepte of het niveau van een knoop is de afstand tussen de wortel en de knoop in kwestie.
  • H heeft een diepte van 2
  • B heeft een diepte van 1

Een eenvoudige boomstructuur implementeren

Zoals we eerder zagen, is een boomknoop niet meer dan een datastructuur met een waarde en links naar zijn afstammelingen.

Hier volgt een voorbeeld van een boomnode:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

We kunnen als volgt een boom met 3 afstammelingen maken:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Dat is alles; we hebben een boom-gegevensstructuur!

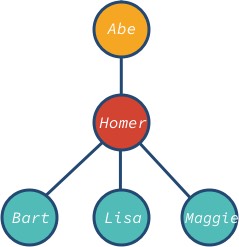
Het knooppunt abe is de wortel en bart, lisa en maggie zijn de bladknooppunten van de boom. Merk op dat de boomknopen verschillende afstammelingen kunnen hebben: 0, 1, 3, of elke andere waarde.

Gegevensstructuren in bomen kennen vele toepassingen, zoals:

• Kaarten
• Sets
• Databases
• Prioriteitsrijen
• Vragen naar een LDAP (Lightweight Directory Access Protocol)
• Voorstellen van het Document Object Model (DOM) voor HTML op Websites.

Binaire bomen

Bomenknopen kunnen nul of meer kinderen hebben. Heeft een boom echter hooguit twee kinderen, dan spreekt men van een binaire boom.

Volledige, complete en perfecte binaire bomen

Afhankelijk van hoe de knooppunten in een binaire boom zijn gerangschikt, kan deze volledig, compleet en perfect zijn:

• Volledige binaire boom: elk knooppunt heeft precies 0 of 2 kinderen (maar nooit 1).
• Volledige binaire boom: als alle niveaus behalve het laatste vol zijn met knopen.
• Perfecte binaire boom: als alle niveaus (ook het laatste) vol zijn met knopen.

Kijk eens naar deze voorbeelden:

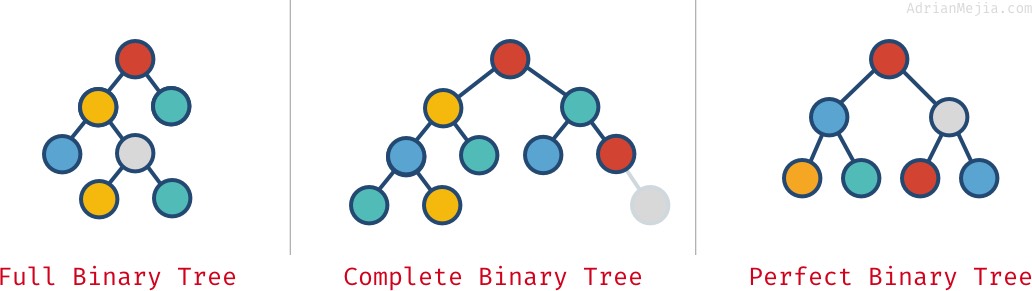
Deze eigenschappen sluiten elkaar niet altijd uit. Je kunt er meer dan één hebben:

• Een perfecte boom is altijd compleet en vol.
  • Perfecte binaire bomen hebben precies `2^k – 1` knopen, waarbij k het laatste niveau van de boom is (beginnend met 1).
• Een complete boom is niet altijd full.
  • Zoals in ons “complete” voorbeeld, omdat het een ouder heeft met slechts één kind. Als we de meest rechtse grijze knoop verwijderen, dan zouden we een complete en volledige boom hebben, maar niet perfect.
• Een volledige boom is niet altijd compleet en perfect.

Binaire zoekboom (BST)

Binaire zoekbomen of kortweg BST zijn een bijzondere toepassing van binaire bomen. BST heeft ten hoogste twee knooppunten (zoals alle binaire bomen). De waarden zijn echter zo dat de waarde van de linker kinderen lager moet zijn dan die van de ouder, en de waarde van de rechter kinderen hoger.

Duplicaten: Sommige BST staan geen duplicaten toe, terwijl andere dezelfde waarden als een rechterkind toevoegen. Andere implementaties zouden een telling kunnen bijhouden van een geval van duplicatie (we gaan dit later doen).

Laten we een Binaire Zoekboom implementeren!

Implementatie van BST

BST lijken erg op onze vorige implementatie van een boom. Er zijn echter enkele verschillen:

• Nodes kunnen hooguit twee kinderen hebben: links en rechts.
• Nodes waarden moeten worden geordend als left < parent < right.

Hier is de boomknoop. Lijkt erg op wat we eerder deden, maar we hebben wat handige getters en setters toegevoegd voor de linker en rechter kinderen. Merk op dat er ook een verwijzing naar de ouder wordt bijgehouden, en dat we deze bijwerken telkens wanneer we kinderen toevoegen.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Ok, tot nu toe kunnen we een links en rechts kind toevoegen. Laten we nu de BST-klasse uitvoeren die de left < parent < right-regel afdwingt.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Laten we het invoegen implementeren.

BST Node Insertion

Om een node in een binaire boom in te voegen, doen we het volgende:

1. Als een boom leeg is, wordt de eerste node de root, en bent u klaar.
2. Vergelijk de waarde van de root met die van de parent. Als deze hoger is, ga dan naar rechts, als deze lager is, ga dan naar links. Als het hetzelfde is, dan bestaat de waarde al, zodat je het aantal duplicaten kunt verhogen (multipliciteit).
3. Herhaal #2 tot we een leeg slot hebben gevonden om de nieuwe node in te voegen.

Laten we eens illustreren hoe u 30, 40, 10, 15, 12, 50 kunt invoegen:

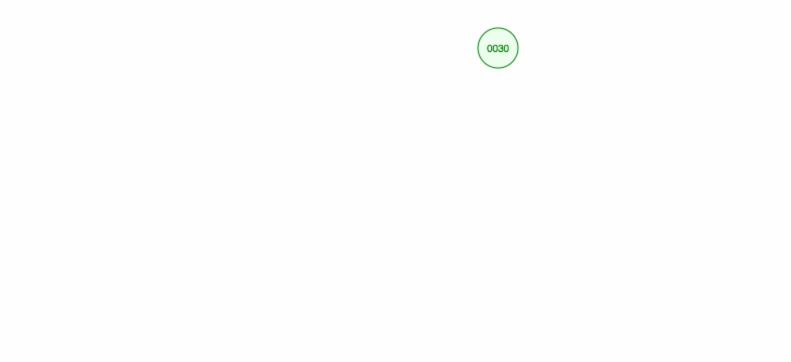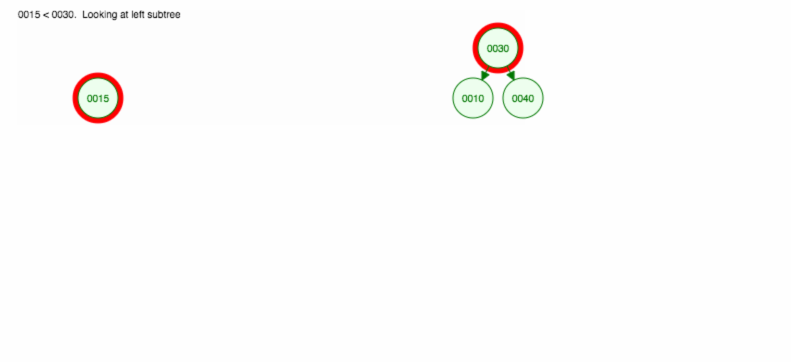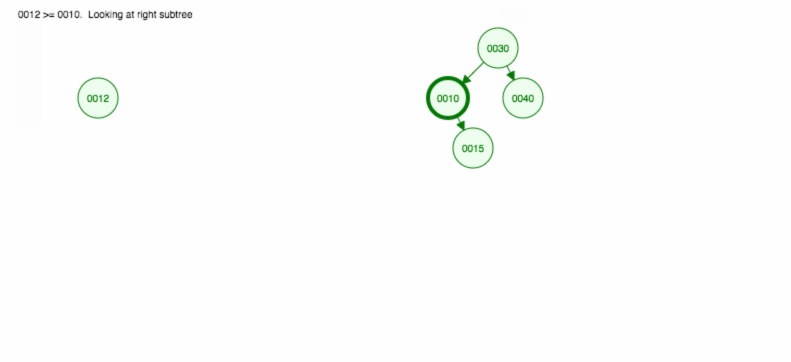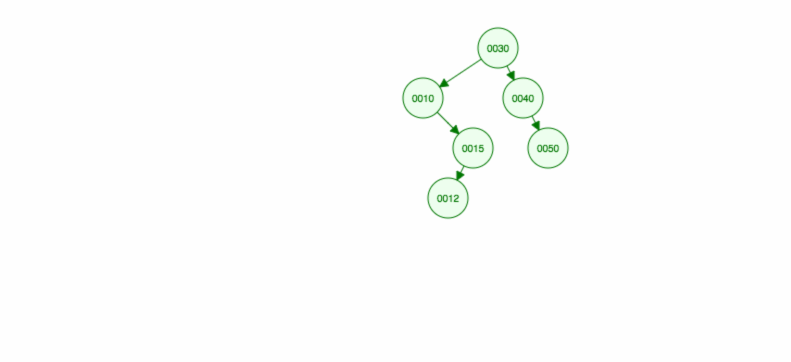
We kunnen invoegen als volgt implementeren:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

We gebruiken een helperfunctie met de naam findNodeAndParent. Als we ontdekken dat het knooppunt al bestaat in de boom, dan verhogen we de teller multiplicity. Laten we eens kijken hoe deze functie is geïmplementeerd:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent gaat door de boom, op zoek naar de waarde. Hij begint bij de wortel (regel 2) en gaat dan naar links of rechts, afhankelijk van de waarde (regel 10). Als de waarde al bestaat, wordt het knooppunt found en ook de ouder teruggegeven. In het geval dat de node niet bestaat, retourneren we nog steeds de parent.

BST Node Deletion

We weten hoe we de waarde moeten invoegen en zoeken. Nu gaan we de verwijder operatie implementeren. Het is een beetje lastiger dan toevoegen, dus laten we het uitleggen met de volgende gevallen:

Een bladknooppunt verwijderen (0 kinderen)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

We verwijderen de verwijzing van de ouder van het knooppunt (15) om null te zijn.

Een knooppunt met één kind verwijderen.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

In dit geval gaan we naar de ouder (30) en vervangen we het kind (10) door het kind van een kind (15).

Een knooppunt met twee kinderen verwijderen

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

We verwijderen knooppunt 40, dat twee kinderen heeft (35 en 50). We vervangen het kind (30) van de ouder (40) door het rechterkind van het kind (50). Vervolgens houden we het linkerkind (35) op dezelfde plaats als voorheen, zodat het het linkerkind van 50 wordt.

Een andere manier om knooppunt 40 te verwijderen is door het linkerkind (35) naar boven te verplaatsen en vervolgens het rechterkind (50) te houden waar het was.

1
2
3
4
5

 30
/ \
15 35
\
50

Een van beide manieren is goed, zolang je maar de eigenschap van de binaire zoekboom behoudt: left < parent < right.

De wortel verwijderen.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

De wortel verwijderen lijkt erg op het eerder besproken verwijderen van knooppunten met 0, 1, of 2 kinderen. Het enige verschil is dat we daarna de referentie van de wortel van de boom moeten bijwerken.

Hier volgt een animatie van wat we hebben besproken.

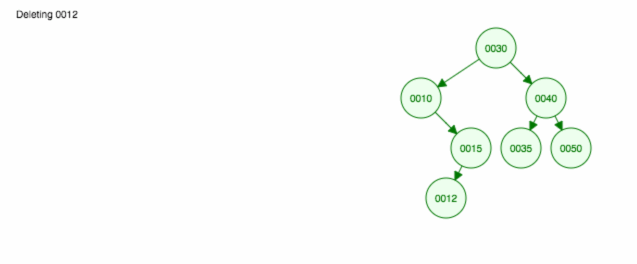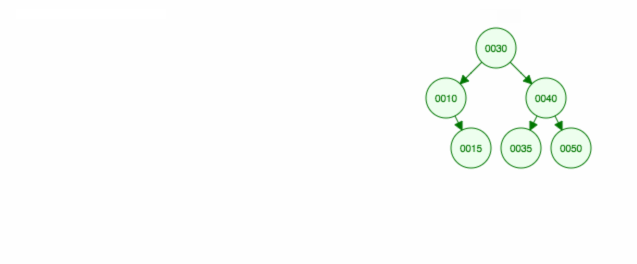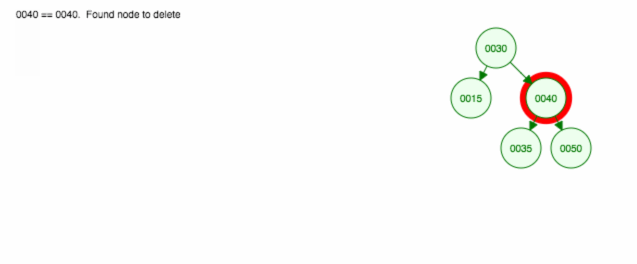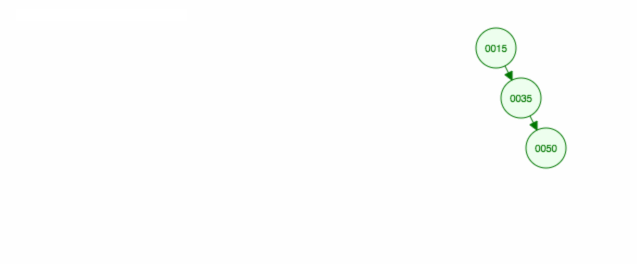
De animatie schuift het linker kind/de linker subboom omhoog en houdt het rechter kind/de rechter subboom op zijn plaats.

Nu we een goed idee hebben hoe het moet werken, laten we het implementeren:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Hier volgen enkele hoogtepunten uit de implementatie:

• Eerst zoeken we of het knooppunt bestaat. Als dat niet het geval is, retourneren we false en zijn we klaar!
• Als het te verwijderen knooppunt bestaat, worden de linker en rechter kinderen gecombineerd tot één subtree.
• Vervang het te verwijderen knooppunt met de gecombineerde subtree.

De functie die de linker in de rechter subtree combineert, is de volgende:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Stel bijvoorbeeld dat we de volgende boom willen combineren en dat we op het punt staan om knooppunt 30 te verwijderen. We willen de linker subtree van de 30 mengen met de rechter. Het resultaat is als volgt:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Als we de nieuwe deelboom de wortel maken, dan is node 30 niet meer!

Binary Tree Transversal

Er zijn verschillende manieren om een Binary Tree te doorkruisen, afhankelijk van de volgorde waarin de knooppunten worden bezocht: in-order, pre-order, en post-order. We kunnen ook deDFSenBFS gebruiken die we hebben geleerd in de grafiekpost.Laten we ze allemaal doorlopen.

In-Order Traversal

In-order traversal bezoekt knooppunten in deze volgorde: links, bovenliggend, rechts.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Laten we deze boom gebruiken om het voorbeeld te maken:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

In-order traversal zou de volgende waarden worden afgedrukt: 3, 4, 5, 10, 15, 30, 40. Als de boom een BST is, worden de knooppunten in stijgende volgorde gesorteerd, zoals in ons voorbeeld.

Post-order traversal

Post-order traversal bezoekt knooppunten in deze volgorde: links, rechts, bovenliggend.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversal zou de volgende waarden uitdrukken: 3, 4, 5, 15, 40, 30, 10.

Pre-Order Traversal en DFS

Pre-order traversal bezoekt nodes in deze volgorde: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversal zou de volgende waarden uitdrukken: 10, 5, 4, 3, 30, 15, 40. Deze volgorde van getallen is hetzelfde resultaat dat we zouden krijgen als we de Depth-First Search (DFS) zouden uitvoeren.

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Als u een opfrisser nodig hebt over DFS, hebben we dit in detail behandeld in Graph post.

Breadth-First Search (BFS)

Gelijk aan DFS kunnen we een BFS implementeren door de Stack te vervangen door een Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

De BFS-volgorde is: 10, 5, 30, 4, 15, 40, 3

Gebalanceerde vs. Niet gebalanceerde bomen

Tot nu toe hebben we besproken hoe add, remove, en find elementen. We hebben het echter nog niet gehad over runtimes. Laten we eens nadenken over de slechtst denkbare scenario’s.

Laten we zeggen dat we getallen willen optellen in oplopende volgorde.

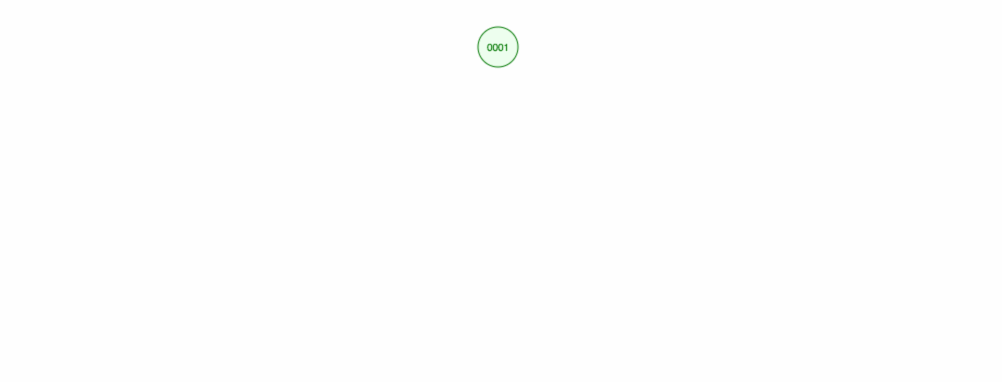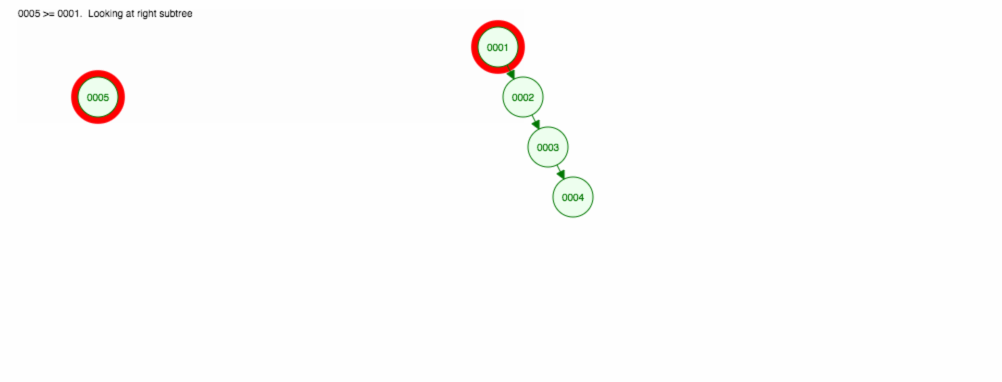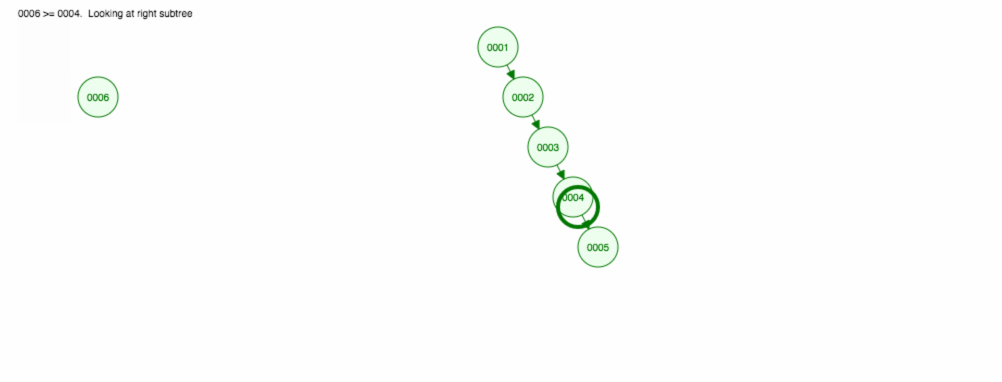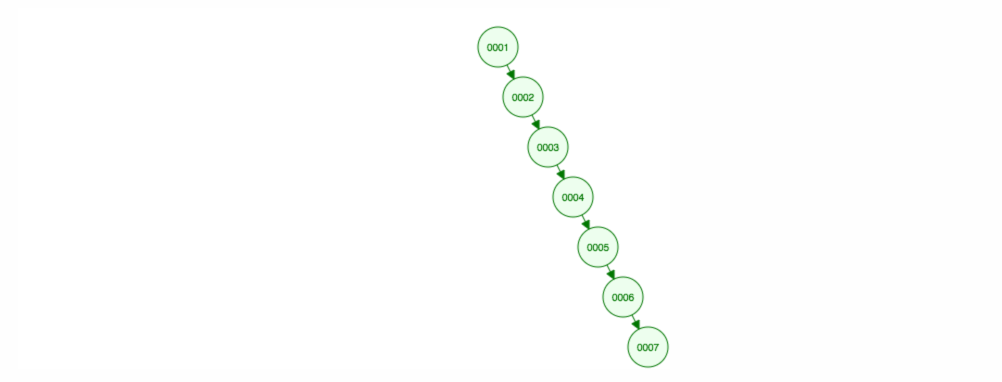
We zullen eindigen met alle knooppunten aan de rechterkant! Deze onevenwichtige boom is niet beter dan een LinkedList, dus het vinden van een element zou O(n) kosten. 😱

Het zoeken van iets in een ongebalanceerde boom is als het zoeken van een woord in het woordenboek bladzijde voor bladzijde. Als de boom in balans is, kun je het woordenboek in het midden openen, en van daaruit weet je of je naar links of naar rechts moet gaan, afhankelijk van het alfabet en het woord dat je zoekt.

We moeten een manier vinden om de boom in balans te brengen!

Als de boom in balans was, zouden we elementen kunnen vinden in O(log n) in plaats van elk knooppunt af te gaan. Laten we eens bekijken wat een gebalanceerde boom betekent.

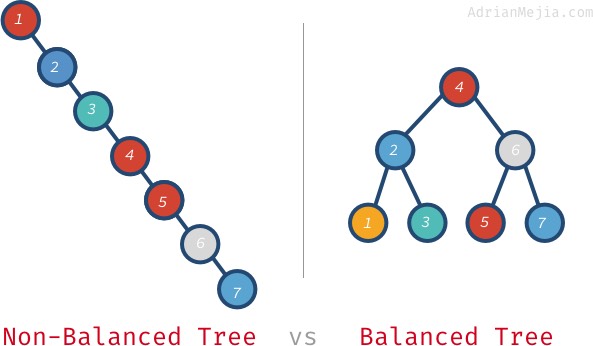
Als we 7 zoeken in de niet-gebalanceerde boom, moeten we van 1 naar 7. In de gebalanceerde boom echter, bezoeken we: 4, 6, en 7. Het wordt nog erger met grotere bomen. Als je een miljoen nodes hebt, kan het zoeken naar een niet-bestaand element je verplichten om alle miljoenen te bezoeken, terwijl je in een gebalanceerde boom. Het heeft maar 20 bezoeken nodig! Dat is een enorm verschil!

We gaan dit probleem oplossen in de volgende post met behulp van zelf-geëvenwichte bomen (AVL trees).

Samenvatting

We hebben veel besproken over bomen. Laten we het samenvatten met opsommingstekens:

• De boom is een gegevensstructuur waarin een knooppunt 0 of meer afstammelingen/kinderen heeft.
• Boomknooppunten hebben geen cycli (acyclisch). Als het cycli heeft, is het in plaats daarvan een Graph datastructuur.
• Bomen met twee kinderen of minder worden genoemd: Binary Tree
• Wanneer een Binary Tree zo wordt gesorteerd dat de linker waarde lager is dan de ouder en de rechter kinderen hoger, dan en alleen dan hebben we een Binary Search Tree.
• Je kunt een boom bezoeken op een pre/post/in-order mode.
• Een ongebalanceerde heeft een tijdcomplexiteit van O(n). 🤦🏻
• Een gebalanceerde heeft een tijdcomplexiteit van O(log n). 🎉