Puutietorakenteilla on monia käyttötarkoituksia, ja niiden toiminnasta on hyvä olla perusymmärrys. Puut ovat perusta muille paljon käytetyille tietorakenteille, kuten Kartat ja Joukot. Lisäksi niitä käytetään tietokannoissa nopeiden hakujen tekemiseen. HTML DOM käyttää puurakennetta elementtien hierarkian esittämiseen. Tässä postauksessa tutustutaan erityyppisiin puihin, kuten binääripuihin, binäärihakupuihin ja niiden toteuttamiseen.

Edellisessä postauksessa tutustuimme graafitietorakenteisiin, jotka ovat puiden yleistetty tapaus. Aloitetaan opettelemalla, mitä puun tietorakenteet ovat!

Tämä postaus on osa tutoriaalisarjaa:

Tietorakenteiden ja algoritmien (DSA) oppiminen aloittelijoille

1. Esittely algoritmin aikakompleksisuuteen ja Big O -merkintätapaukseen

2. Kahdeksan aikakompleksisuutta, jotka jokaisen ohjelmoijan tulisi tuntea

3. Tietorakenteet aloittelijoille:

4. Graafin tietorakenteet aloittelijoille

5. Puiden tietorakenteet aloittelijoille 👈 olet täällä

6. Self-balanced Binary Search Trees

7. Liite I: Analysis of Recursive Algorithms

Puut: peruskäsitteitä

Puu on tietorakenne, jossa solmulla voi olla nolla tai useampia lapsia. Jokainen solmu sisältää arvon. Kuten graafeissa, solmujen välisiä yhteyksiä kutsutaan reunoiksi. Puu on eräänlainen graafi, mutta kaikki graafit eivät ole puita (siitä lisää myöhemmin).

Näitä tietorakenteita kutsutaan ”puiksi”, koska tietorakenne muistuttaa puuta 🌳. Se alkaa juurisolmusta ja haarautuu sen jälkeläisillä, ja lopuksi on lehdet.

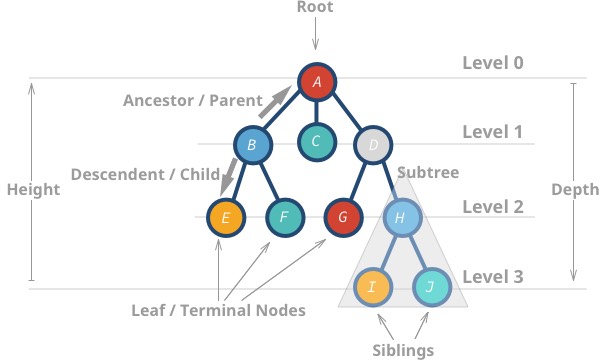
Tässä on joitain puiden ominaisuuksia:

• Huippusolmua kutsutaan juureksi.
• Solmua, jolla ei ole lapsia, kutsutaan lehtisolmuksi tai päätepisteen solmuksi.
• Puun korkeus (h) on etäisyys (reunojen lukumäärä) kauimmaisen lehden ja juuren välillä.
  • A korkeus on 3
  • I korkeus on 0
• Solmun syvyys tai taso on etäisyys juuren ja kyseisen solmun välillä.
  • H on syvyys 2
  • B on syvyys 1

Yksinkertaisen puun tietorakenteen toteuttaminen

Kuten aiemmin näimme, puun solmu on pelkkä tietorakenne, jolla on arvo ja linkit sen jälkeläisiin.

Tässä on esimerkki puun solmusta:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Voimme luoda puun, jolla on 3 jälkeläistä, seuraavasti:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Siinä kaikki; meillä on puumainen tietorakenne!

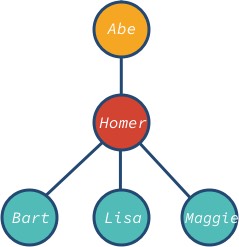
Solmu abe on juuri ja bart, lisa ja maggie ovat puun lehtisolmut. Huomaa, että puun solmulla voi olla erilaisia jälkeläisiä: 0, 1, 3 tai mikä tahansa muu arvo.

Puiden tietorakenteilla on monia sovelluksia, kuten:

• Kartat
• joukot
• Tietokannat
• Prioriteettiluettelot
• Kysely LDAP:stä (kevyt hakemistoprotokollasta)
• Dokumenttiobjekti-mallin (Document Object Model, DOM) esittely HTML:ää varten verkkosivustoilla.

Binääripuut

Puiden solmuilla voi olla nolla tai enemmän lapsia. Kun puulla on kuitenkin korkeintaan kaksi lasta, sitä kutsutaan binääripuuksi.

Täydelliset, täydelliset ja täydelliset binääripuut

Riippuen siitä, miten solmut on järjestetty binääripuussa, se voi olla täysi, täydellinen ja täydellinen:

• Täydellinen binääripuu: jokaisella solmulla on täsmälleen 0 tai 2 lasta (mutta ei koskaan 1).
• Täydellinen binääripuu: kun kaikki tasot viimeistä lukuun ottamatta ovat täynnä solmuja.
• Täydellinen binääripuu: kun kaikki tasot (viimeinen mukaan lukien) ovat täynnä solmuja.

Katsokaa näitä esimerkkejä:

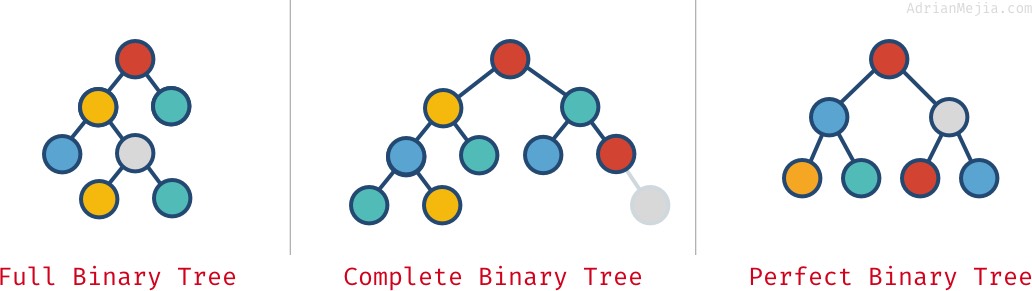
Näillä ominaisuuksilla ei aina ole toisiaan poissulkevia vaikutuksia. Niitä voi olla useampia:

• Täydellinen puu on aina täydellinen ja täysi.
  • Täydellisillä binääripuilla on täsmälleen `2^k – 1` solmuja, missä k on puun viimeinen taso (alkaen 1:stä).
• Täydellinen puu ei ole aina full.
  • Kuten ”täydellisessä”-esimerkissämme, koska sillä on vanhempi, jolla on vain yksi lapsi. Jos poistamme oikeanpuoleisimman harmaan solmun, saamme täydellisen ja täyden puun, mutta emme täydellistä.
• Täydellinen puu ei ole aina täydellinen ja täydellinen.

Binäärinen hakupuu (BST)

Binääriset hakupuut tai lyhyesti BST ovat binääripuiden erityinen sovellus. BST:llä on korkeintaan kaksi solmua (kuten kaikilla binääripuilla). Arvot ovat kuitenkin niin, että vasemman lapsen arvon on oltava pienempi kuin vanhemman ja oikean lapsen arvon on oltava suurempi.

Duplikaatit: Jotkut BST:t eivät salli duplikaatteja, kun taas toiset lisäävät samat arvot oikeaksi lapseksi. Toiset toteutukset saattavat pitää lukua päällekkäisyystapauksesta (teemme tämän myöhemmin).

Toteutetaan binäärihakupuu!

BST:n toteutus

BST:t ovat hyvin samankaltaisia kuin aiempi puun toteutuksemme. On kuitenkin joitain eroja:

• Solmuilla voi olla korkeintaan vain kaksi lasta: vasen ja oikea.
• Solmujen arvot on järjestettävä left < parent < right.

Tässä on puun solmu. Hyvin samanlainen kuin mitä teimme aiemmin, mutta lisäsimme muutamia käteviä gettereitä ja settereitä vasemmalle ja oikealle lapselle. Huomaa pitää myös viittauksen vanhempaan, ja päivitämme sen aina kun lisäämme lapsia.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Okei, tähän mennessä voimme lisätä vasemman ja oikean lapsen. Nyt tehdään BST-luokka, joka panee left < parent < right-säännön täytäntöön.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Toteutetaan lisäys.

BST-solmun lisääminen

Solmun lisääminen binääripuuhun tapahtuu seuraavasti:

1. Jos puu on tyhjä, ensimmäisestä solmusta tulee juuri, ja olet valmis.
2. Vertaile juuren ja vanhemman arvoa, jos se on korkeampi, siirry oikealle, jos matalampi, siirry vasemmalle. Jos se on sama, niin arvo on jo olemassa, joten voit lisätä kaksoiskappaleiden lukumäärää (multiplicity).
3. Toista #2, kunnes löysimme tyhjän paikan uuden solmun lisäämiseksi.

Tehdään havainnollistus, miten lisätään 30, 40, 10, 15, 12, 50:

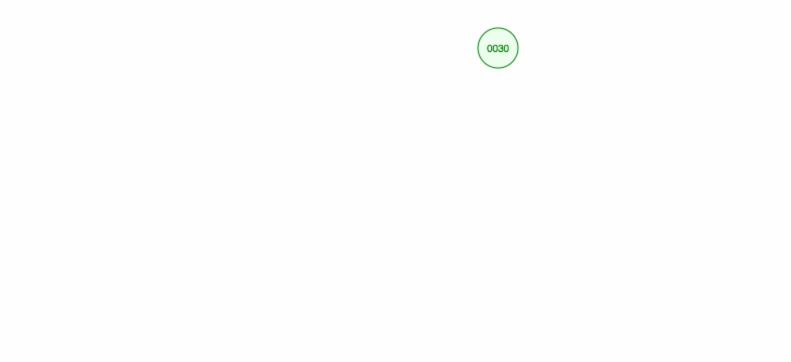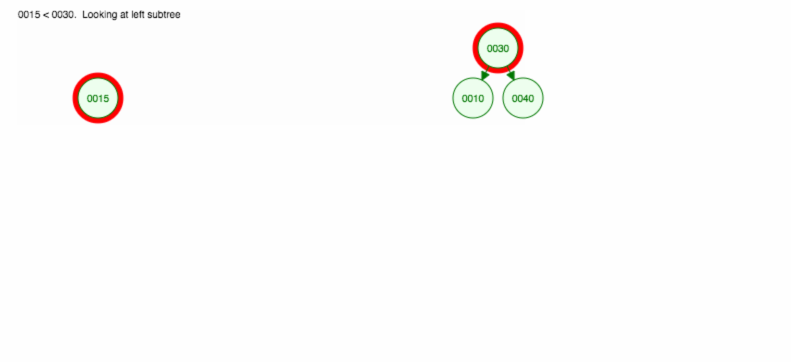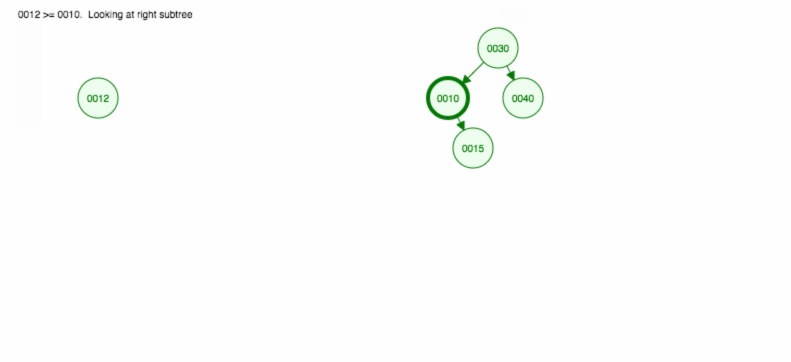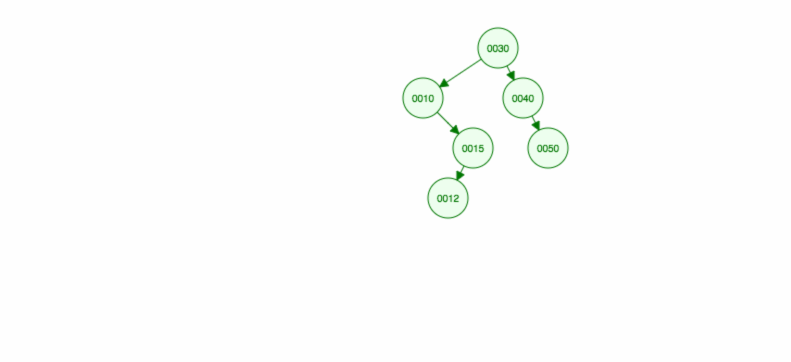
Voidaan toteuttaa insert seuraavasti:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Käytämme apufunktiota findNodeAndParent. Jos havaitsemme, että solmu on jo olemassa puussa, kasvatamme multiplicity-laskuria. Katsotaanpa, miten tämä funktio on toteutettu:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent käy läpi puun etsien arvon. Se aloittaa juuresta (rivi 2) ja siirtyy sitten vasemmalle tai oikealle arvon perusteella (rivi 10). Jos arvo on jo olemassa, se palauttaa solmun found ja myös vanhemman. Jos solmua ei ole olemassa, palautetaan silti parent.

BST-solmun poisto

Me tiedämme, miten arvo lisätään ja etsitään. Nyt toteutamme poisto-operaation. Se on hieman hankalampi kuin lisääminen, joten selitetään se seuraavien tapausten avulla:

Lehtisolmun (0 lasta)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Poistamme viittauksen solmun vanhemmasta (15) nollaksi.

Solmun, jolla on yksi lapsi, poistaminen.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

Tässä tapauksessa siirrymme vanhempaan (30) ja korvaamme lapsen (10) lapsen lapsella (15).

Poistetaan solmu, jolla on kaksi lasta

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Poistamme solmun 40, jolla on kaksi lasta (35 ja 50). Korvaamme vanhemman (30) lapsen (40) lapsen oikealla lapsella (50). Sitten pidämme vasemman lapsen (35) samassa paikassa kuin ennenkin, joten meidän on tehtävä siitä 50:n vasen lapsi.

Toinen tapa poistaa solmu 40 on siirtää vasen lapsi (35) ylöspäin ja pitää sitten oikea lapsi (50) paikallaan.

1
2
3
4
5

 30
/ \
15 35
\
50

Kumpikin tapa on ok, kunhan säilytetään binäärihakupuun ominaisuus: left < parent < right.

Juuren poistaminen.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Juuren poistaminen on hyvin samankaltaista kuin aiemmin käsitelty sellaisten solmujen poistaminen, joilla on 0, 1 tai 2 lasta. Ainoa ero on, että sen jälkeen on päivitettävä puun juuren viittaus.

Tässä on animaatio siitä, mistä keskustelimme.

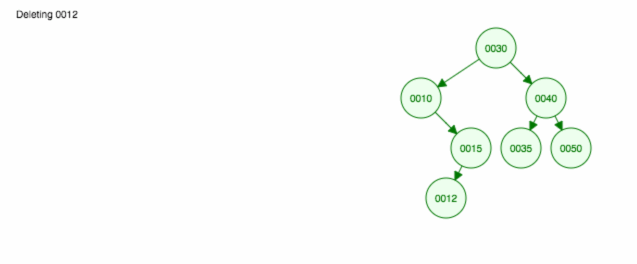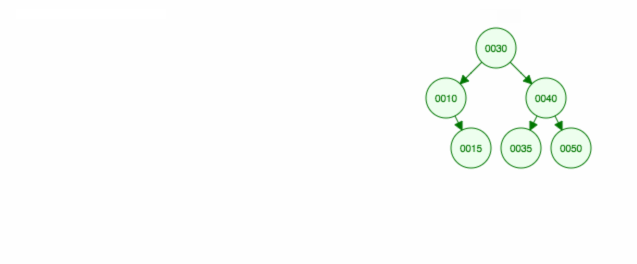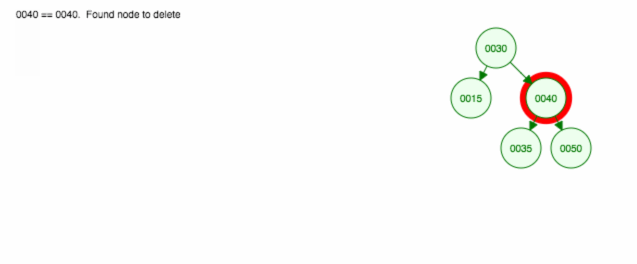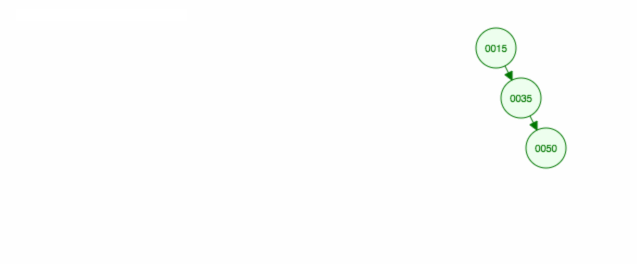
Animaatio siirtää vasemmanpuoleista lasta/alipuuta ylöspäin ja pitää oikeanpuoleisen lapsen/alipuun paikallaan.

Nyt kun meillä on hyvä käsitys siitä, miten sen pitäisi toimia, toteutetaan se:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Tässä on joitain kohokohtia toteutuksesta:

• Ensin etsitään, onko solmu olemassa. Jos ei ole, palautamme false, ja olemme valmiit!
• Jos poistettava solmu on olemassa, yhdistetään vasen ja oikea lapsi yhdeksi alipuuksi.
• Poistettava solmu korvataan yhdistetyllä alipuulla.

Funktio, joka yhdistää vasemman alipuun oikeaksi alipuuksi, on seuraavanlainen:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Esitettäköön esimerkiksi, että haluamme yhdistää seuraavan puun ja olemme poistamassa solmua 30. Haluamme yhdistää 30:n vasemmanpuoleisen alipuun oikeanpuoleiseen alipuuhun. Tulos on tämä:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Jos teemme uudesta osapuusta juuren, solmua 30 ei enää ole!

Binääripuun läpikäynti

Binääripuun läpikäyntiin on erilaisia tapoja riippuen siitä, missä järjestyksessä solmut käydään läpi: in-order, pre-order ja post-order. Voimme myös käyttää niitäDFSjaBFSjoita opimmegraph post.käydään läpi kukin.

In-order Traversal

In-order traversal visit nodes on this order: left, parent, right.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Käytetään tätä puuta esimerkin tekemiseen:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

Järjestyksessä tapahtuva läpikäynti tulostaisi seuraavat arvot: 3, 4, 5, 10, 15, 30, 40. Jos puu on BST, solmut lajitellaan nousevaan järjestykseen kuten esimerkissämme.

Post-order traversal

Post-order traversal käy solmujen luona tässä järjestyksessä: left, right, parent.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversal tulostaisi seuraavat arvot: 3, 4, 5, 15, 40, 30, 10.

Pre-order traversal and DFS

Pre-order traversal visit nodes on this order: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversal tulostaisi seuraavat arvot: 10, 5, 4, 3, 30, 15, 40. Tämä lukujärjestys on sama tulos, jonka saisimme, jos suorittaisimme syvyyssuuntaisen haun (Depth-First Search, DFS).

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Jos kaipaat kertausta DFS:stä, käsiteltiin sitä yksityiskohtaisesti Graph-postissa.

Breadth-First Search (BFS)

Samankaltaisesti kuin DFS, voimme toteuttaa BFS:n vaihtamalla Stack:n Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

BFS-järjestys on: 10, 5, 30, 4, 15, 40, 3

Tasapainotetut vs. ei-tasapainotetut puut

Tähän mennessä olemme käsitelleet, miten add, remove ja find elementtejä. Emme ole kuitenkaan puhuneet ajoajoista. Mietitäänpä huonoimpia skenaarioita.

Asettakaamme, että haluamme lisätä numeroita nousevassa järjestyksessä.

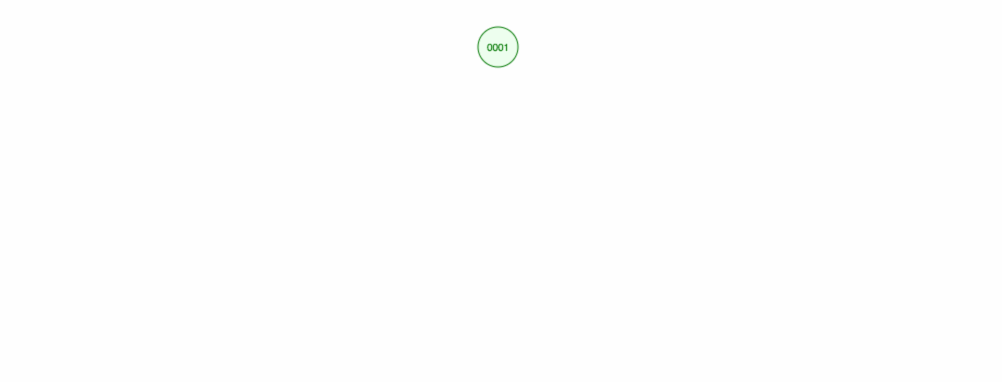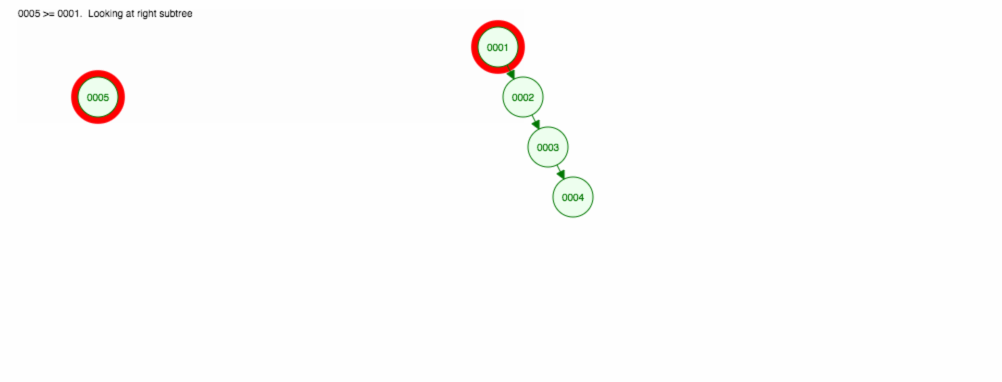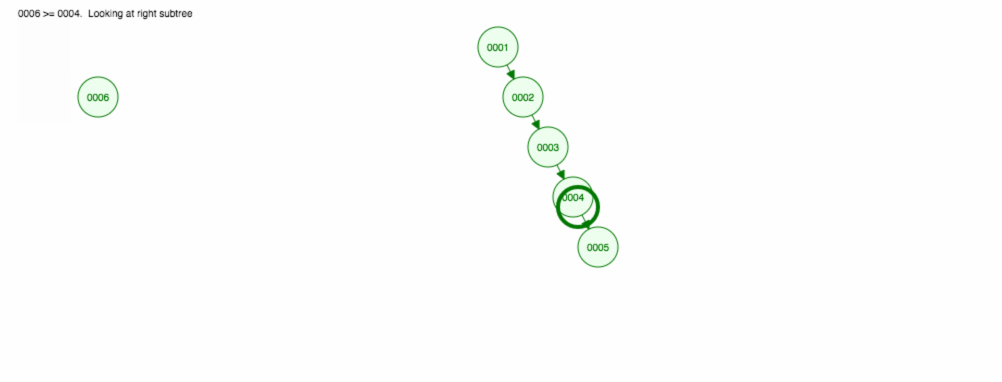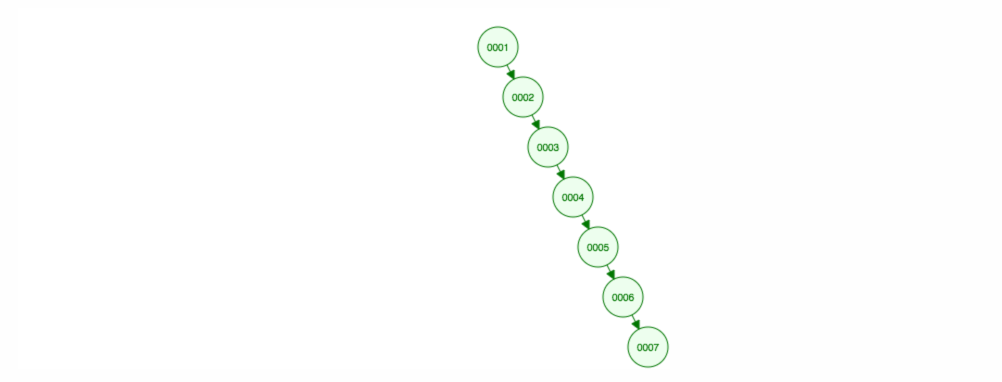
Päädymme siihen, että kaikki solmut ovat oikealla puolella! Tämä epätasapainoinen puu ei ole yhtään parempi kuin LinkedList, joten elementin löytäminen veisi aikaa O(n). 😱

Etsiminen epätasapainoisesta puusta on kuin etsisi sanaa sanakirjasta sivu kerrallaan. Kun puu on tasapainossa, voit avata sanakirjan keskeltä, ja sieltä tiedät, onko sinun mentävä vasemmalle vai oikealle riippuen aakkosista ja etsimästäsi sanasta.

Meidän on löydettävä keino tasapainottaa puu!

Jos puu olisi tasapainossa, voisimme löytää elementtejä O(log n):ssä sen sijaan, että kävisimme jokaisen solmun läpi. Puhutaanpa siitä, mitä tasapainoinen puu tarkoittaa.

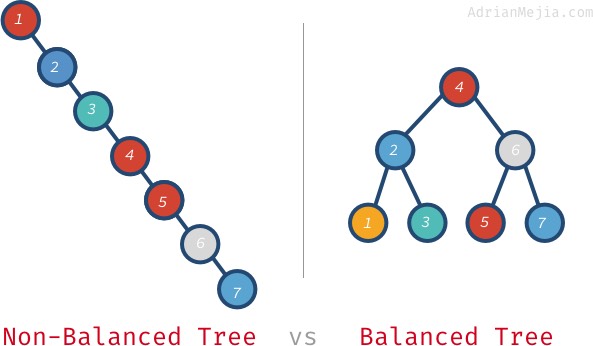
Jos etsimme 7 ei-tasapainoisessa puussa, meidän on mentävä 1:stä 7:ään. Tasapainoisessa puussa käymme kuitenkin: 4, 6 ja 7. Tilanne pahenee entisestään suuremmissa puissa. Jos solmuja on miljoona, ei-olemassa olevan elementin etsiminen saattaa vaatia käyntiä kaikissa miljoonissa solmuissa tasapainoisessa puussa. Se tarvitsee vain 20 käyntiä! Se on valtava ero!

Ratkaisemme tämän ongelman seuraavassa postauksessa käyttämällä itsetasapainottuneita puita (AVL-puita).

Yhteenveto

Olemme käsitelleet paljon puita. Tiivistetään se luoteihin:

• Puu on tietorakenne, jossa solmulla on 0 tai useampi jälkeläinen/lapsi.
• Puun solmuilla ei ole syklejä (asyklisiä). Jos sillä on syklejä, se on sen sijaan Graph-tietorakenne.
• Puita, joilla on kaksi lasta tai vähemmän, kutsutaan: Binääripuu
• Kun binääripuu lajitellaan niin, että vasemmanpuoleinen arvo on pienempi kuin vanhemman ja oikeanpuoleinen lasten arvo on suurempi, silloin ja vain silloin meillä on binääripuu.
• Puussa voi käydä ennen/jälkeen/järjestyksessä.
• Tasapainottoman puun aikakompleksisuus on O(n). 🤦🏻
• Tasapainoisella on aikakompleksisuus O(log n). 🎉