Posted on

Adrian Mejia

, Author

Structurile de date arborescente au multe utilizări și este bine să aveți o înțelegere de bază a modului în care acestea funcționează. Arborii sunt baza pentru alte structuri de date foarte utilizate, cum ar fi Maps și Sets. De asemenea, ei sunt utilizați în bazele de date pentru a efectua căutări rapide. HTML DOM utilizează o structură de date de tip arbore pentru a reprezenta ierarhia elementelor. Această postare va explora diferitele tipuri de arbori, cum ar fi arborii binari, arborii de căutare binară, și cum să le implementăm.

Am explorat structurile de date Graph în postarea anterioară, care sunt un caz generalizat de arbori. Haideți să începem să învățăm ce sunt structurile de date de tip arbore!

Această postare face parte dintr-o serie de tutoriale:

Învățarea structurilor de date și a algoritmilor (DSA) pentru începători

  1. Introducerea complexității temporale a algoritmilor și notația Big O

  2. Opt complexități temporale pe care orice programator ar trebui să le cunoască

  3. Structuri de date pentru începători: Array-uri, HashMaps și liste

  4. Structuri de date grafice pentru începători

  5. Structuri de date arbori pentru începători 👈 you are here

  6. Arborii de căutare binară autoechilibrată

  7. Anexe I: Analiza algoritmilor recursivi

Arborii: concepte de bază

Un arbore este o structură de date în care un nod poate avea zero sau mai mulți copii. Fiecare nod conține o valoare. Ca și în cazul grafurilor, conexiunea dintre noduri se numește muchii. Un arbore este un tip de graf, dar nu toate grafurile sunt arbori (mai multe despre asta mai târziu).

Aceste structuri de date se numesc „arbori” deoarece structura de date seamănă cu un arbore 🌳. Începe cu un nod rădăcină și se ramifică cu descendenții săi, iar în final, există frunze.

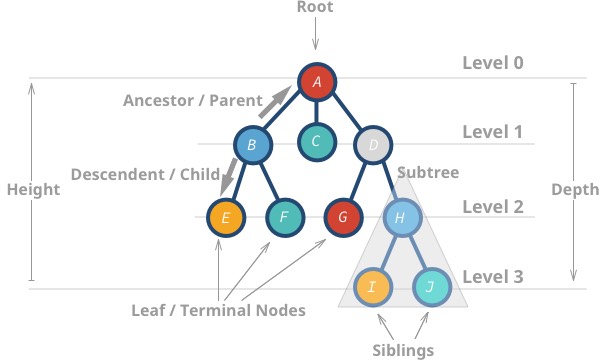
Iată câteva proprietăți ale arborilor:

  • Nodul cel mai de sus se numește rădăcină.
  • Un nod fără copii se numește nod frunză sau nod terminal.
  • Înălțimea (h) arborelui este distanța (numărul de muchii) dintre cea mai îndepărtată frunză și rădăcină.
    • A are o înălțime de 3
    • I are o înălțime de 0
  • Adâncimea sau nivelul unui nod este distanța dintre rădăcină și nodul în cauză.
    • H are o adâncime de 2
    • B are o adâncime de 1

Implementarea unei structuri de date arborescente simple

Așa cum am văzut mai devreme, un nod arborescent este doar o structură de date cu o valoare și legături către descendenții săi.

Iată un exemplu de nod de arbore:

1
2
3
4
5
6
 
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Potem crea un arbore cu 3 descendenți după cum urmează:

1
2
3
4
5
6
7
8
9
10
 
// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Asta este tot; avem o structură de date arborescentă!

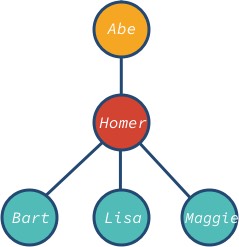
Nodul abe este rădăcina, iar bart, lisa și maggie sunt nodurile frunză ale arborelui. Observați că nodul arborelui poate avea diferiți descendenți: 0, 1, 3 sau orice altă valoare.

Structurile de date de tip arbore au multe aplicații, cum ar fi:

  • Hașele
  • Seturi
  • Baze de date
  • Cozi prioritare
  • Cercetarea unui LDAP (Lightweight Directory Access Protocol)
  • Reprezentarea modelului Document Object Model (DOM) pentru HTML pe site-urile web.

Arbori binari

Nodurile arborilor pot avea zero sau mai mulți copii. Cu toate acestea, atunci când un arbore are cel mult doi copii, atunci se numește arbore binar.

Arbori binari compleți, compleți și perfecți

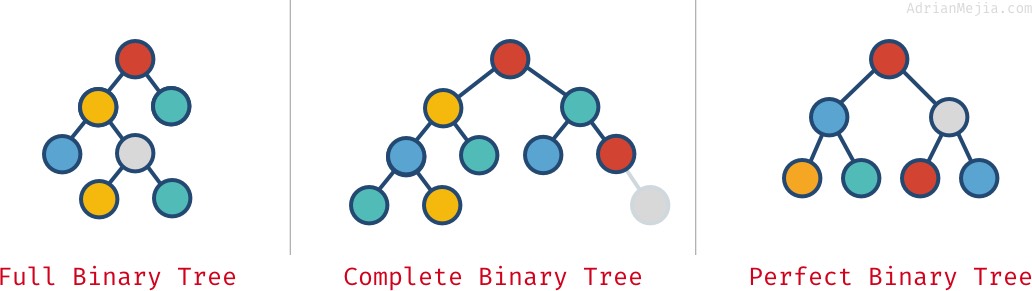
În funcție de modul în care sunt aranjate nodurile într-un arbore binar, acesta poate fi complet, complet și perfect:

  • Arbore binar complet: fiecare nod are exact 0 sau 2 copii (dar niciodată 1).
  • Arbore binar complet: când toate nivelurile, cu excepția ultimului, sunt pline de noduri.
  • Arbore binar perfect: când toate nivelurile (inclusiv ultimul) sunt pline de noduri.

Vezi aceste exemple:

Aceste proprietăți nu se exclud întotdeauna reciproc. Puteți avea mai mult de una:

  • Un arbore perfect este întotdeauna complet și plin.
    • Arborii binari perfecți au exact `2^k – 1` noduri, unde k este ultimul nivel al arborelui (începând cu 1).
  • Un arbore complet nu este întotdeauna full.
    • Ca în exemplul nostru „complet”, deoarece are un părinte cu un singur copil. Dacă eliminăm cel mai din dreapta nod gri, atunci am avea un arbore complet și plin, dar nu perfect.
  • Un arbore complet nu este întotdeauna complet și perfect.

Arborele de căutare binar (BST)

Arborele de căutare binar sau BST, pe scurt, BST este o aplicație particulară a arborilor binari. BST are cel mult două noduri (ca toți arborii binari). Cu toate acestea, valorile sunt astfel încât valoarea copiilor din stânga trebuie să fie mai mică decât cea a părintelui, iar cea a copiilor din dreapta trebuie să fie mai mare.

Duplicat: Unii BST nu permit duplicate, în timp ce alții adaugă aceleași valori ca și copilul din dreapta. Alte implementări ar putea ține cont de un caz de duplicitate (pe acesta îl vom face mai târziu).

Să implementăm un Binary Search Tree!

Implementarea BST

BST sunt foarte asemănătoare cu implementarea noastră anterioară a unui arbore. Cu toate acestea, există câteva diferențe:

  • Nodurile pot avea, cel mult, doar doi copii: stânga și dreapta.
  • Valorile nodurilor trebuie să fie ordonate ca left < parent < right.

Iată nodul arborelui. Foarte asemănător cu ceea ce am făcut înainte, dar am adăugat niște getters și setters la îndemână pentru copiii din stânga și din dreapta. Observați că păstrează, de asemenea, o referință la părinte și o actualizăm de fiecare dată când adăugăm copii.

TreeNode.jsCode
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
 
const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Bine, până acum, putem adăuga un copil stâng și unul drept. Acum, haideți să facem clasa BST care aplică regula left < parent < right.

BinarySearchTree.js linkUrl linkText
1
2
3
4
5
6
7
8
9
10
11
12
13
 

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Să implementăm inserția.

BST Node Insertion

Pentru a insera un nod într-un arbore binar, facem următoarele:

  1. Dacă un arbore este gol, primul nod devine rădăcină și ați terminat.
  2. Comparați valoarea rădăcinii/părintelui dacă este mai mare mergeți la dreapta, dacă este mai mică mergeți la stânga. Dacă este aceeași, atunci valoarea există deja, astfel încât puteți crește numărul de duplicate (multiplicitate).
  3. Repetați #2 până când am găsit un loc gol pentru a introduce noul nod.

Să facem o ilustrare a modului în care se inserează 30, 40, 10, 15, 12, 50:

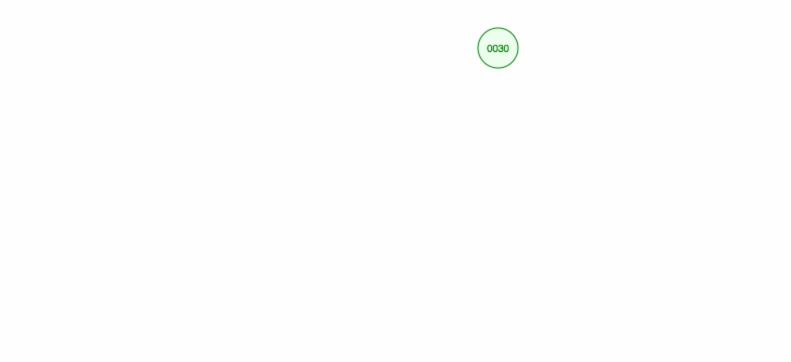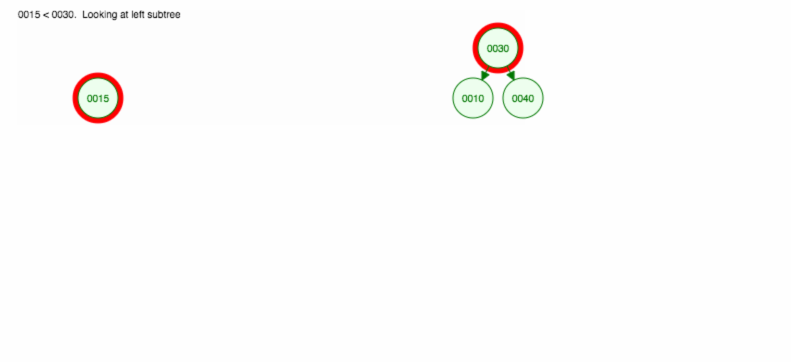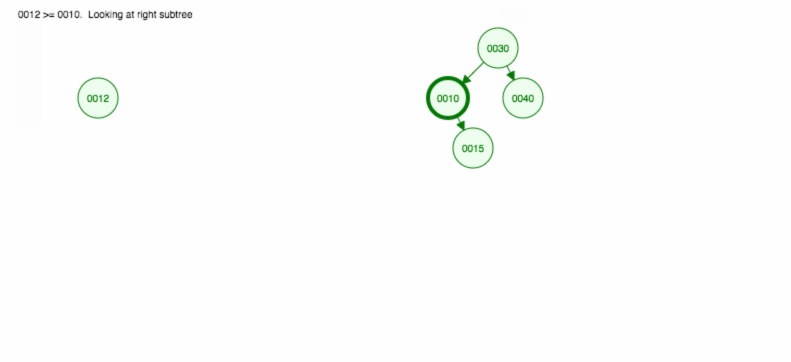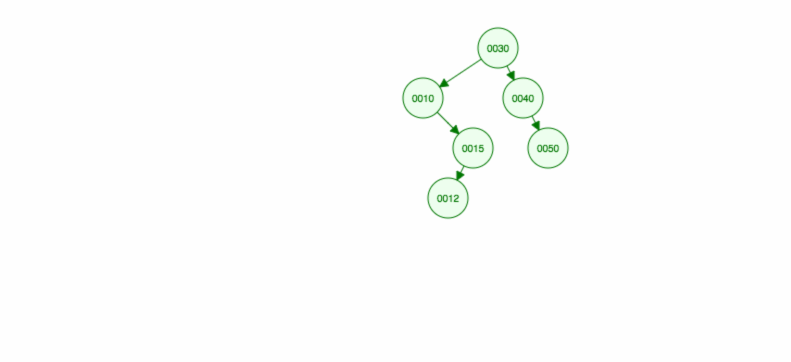
Potem implementa inserarea după cum urmează:

BinarySearchTree.prototype.addFull Cod
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
 
add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Utilizăm o funcție ajutătoare numită findNodeAndParent. Dacă am constatat că nodul există deja în arbore, atunci creștem contorul multiplicity. Să vedem cum este implementată această funcție:

BinarySearchTree.prototype.findNodeAndParentFull Cod
1
2
3
4
5
6
7
8
9
10
11
12
13
14
 
findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent parcurge arborele, căutând valoarea. Acesta începe de la rădăcină (linia 2) și apoi merge spre stânga sau spre dreapta în funcție de valoare (linia 10). În cazul în care valoarea există deja, va returna nodul found și, de asemenea, părintele. În cazul în care nodul nu există, se returnează în continuare parent.

BST Node Deletion

Știm cum să inserăm și să căutăm o valoare. Acum, vom implementa operația de ștergere. Este un pic mai complicat decât adăugarea, așa că vom explica cu următoarele cazuri:

Îndepărtarea unui nod frunză (0 copii)

1
2
3
4
5
6
7
 
 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Îndepărtăm referința de la părintele nodului (15) pentru a fi nulă.

Îndepărtarea unui nod cu un copil.

1
2
3
4
5
 
 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

În acest caz, mergem la părintele (30) și înlocuim copilul (10) cu un copil al copilului (15).

Îndepărtarea unui nod cu doi copii

1
2
3
4
5
 
 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Îndepărtăm nodul 40, care are doi copii (35 și 50). Înlocuim copilul (40) al părintelui (30) cu copilul din dreapta copilului (50). Apoi păstrăm copilul stâng (35) în același loc ca înainte, deci trebuie să-l facem copilul stâng al lui 50.

O altă modalitate de a elimina nodul 40 este să mutăm copilul stâng (35) în sus și apoi să păstrăm copilul drept (50) unde era.

1
2
3
4
5
 
 30
/ \
15 35
\
50

Este în regulă oricare dintre aceste moduri, atâta timp cât se păstrează proprietatea de arbore binar de căutare: left < parent < right.

Îndepărtarea rădăcinii.

1
2
3
4
5
 
 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Îndepărtarea rădăcinii este foarte asemănătoare cu eliminarea nodurilor cu 0, 1 sau 2 copii discutată anterior. Singura diferență este că, după aceea, trebuie să actualizăm referința rădăcinii arborelui.

Iată o animație a ceea ce am discutat.

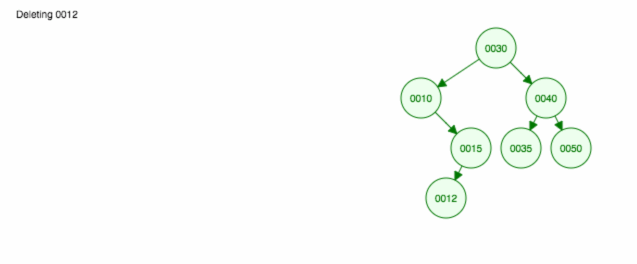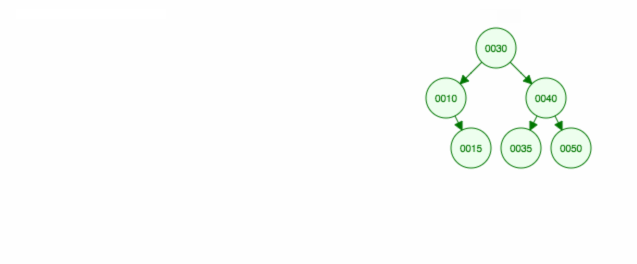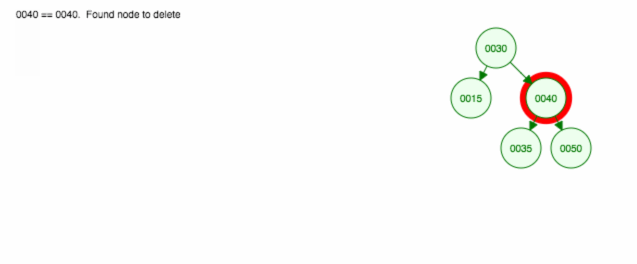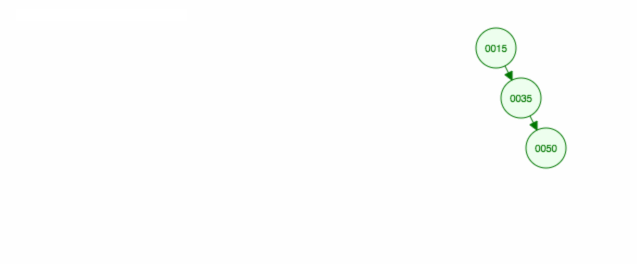
Animația deplasează în sus copilul/subarborele din stânga și păstrează copilul/subarborele din dreapta la locul lui.

Acum că avem o idee bună despre cum ar trebui să funcționeze, haideți să o implementăm:

BinarySearchTree.prototype.removeFull Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
 
remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Iată câteva aspecte importante ale implementării:

    • În primul rând, căutăm dacă nodul există. Dacă nu există, returnăm false și am terminat!
    • Dacă nodul de eliminat există, atunci combinăm copiii din stânga și din dreapta într-un singur subarbore.
    • Înlocuiți nodul de eliminat cu subarborele combinat.

    Funcția care combină subarborele din stânga în cel din dreapta este următoarea:

    BinarySearchTree.prototype.combineLeftIntoRightSubtreeFull Code
    1
    2
    3
    4
    5
    6
    7
    8
    		 
    combineLeftIntoRightSubtree(node) {
    if (node.right) {
    const leftmost = this.getLeftmost(node.right);
    leftmost.left = node.left;
    return node.right;
    }
    return node.left;
    }

    De exemplu, să spunem că dorim să combinăm următorul arbore și suntem pe cale să ștergem nodul 30. Dorim să combinăm subarborele stâng al lui 30 în cel drept. Rezultatul este următorul:

    1
    2
    3
    4
    5
    6
    7
    		 
     30* 40
    / \ / \
    10 40 combine(30) 35 50
    \ / \ -----------> /
    15 35 50 10
    \
    15

    Dacă facem din noul subarbore rădăcina, atunci nodul 30 nu mai există!

    Transversalitatea arborelui binar

    Există diferite moduri de traversare a unui arbore binar, în funcție de ordinea în care sunt vizitate nodurile: în ordine, preordine și postordine. De asemenea, putem folosiDFSșiBFSpe care le-am învățat la postul de graf.Să trecem în revistă fiecare dintre ele.

    Traversarea în ordine

    Traversarea în ordine vizitează nodurile în această ordine: stânga, părinte, dreapta.

    BinarySearchTree.prototype.inOrderTraversalFull Code
    1
    2
    3
    4
    5
    		 
    * inOrderTraversal(node = this.root) {
    if (node.left) { yield* this.inOrderTraversal(node.left); }
    yield node;
    if (node.right) { yield* this.inOrderTraversal(node.right); }
    }

    Să folosim acest arbore pentru a realiza exemplul:

    1
    2
    3
    4
    5
    6
    7
    		 
     10
    / \
    5 30
    / / \
    4 15 40
    /
    3

    O traversare în ordine ar imprima următoarele valori: 3, 4, 5, 10, 15, 30, 40. Dacă arborele este un BST, atunci nodurile vor fi sortate în ordine ascendentă, ca în exemplul nostru.

    Traversarea după ordine

    Traversarea după ordine vizitează nodurile în această ordine: stânga, dreapta, părinte.

    BinarySearchTree.prototype.postOrderTraversalFull Code
    1
    2
    3
    4
    5
    		 
    * postOrderTraversal(node = this.root) {
    if (node.left) { yield* this.postOrderTraversal(node.left); }
    if (node.right) { yield* this.postOrderTraversal(node.right); }
    yield node;
    }

    Post-order traversal ar imprima următoarele valori: 3, 4, 5, 15, 40, 30, 10.

    Pre-Order Traversal and DFS

    Pre-order traversal visit nodes on this order: parent, left, right.

    BinarySearchTree.prototype.preOrderTraversalFull Code
    1
    2
    3
    4
    5
    		 
    * preOrderTraversal(node = this.root) {
    yield node;
    if (node.left) { yield* this.preOrderTraversal(node.left); }
    if (node.right) { yield* this.preOrderTraversal(node.right); }
    }

    Traversarea preordonată ar imprima următoarele valori: 10, 5, 4, 3, 30, 15, 40. Această ordine a numerelor este același rezultat pe care l-am obține dacă am rula Depth-First Search (DFS).

    BinarySearchTree.prototype.dfsFull Code
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    		 
    * dfs() {
    const stack = new Stack();
    stack.add(this.root);
    while (!stack.isEmpty()) {
    const node = stack.remove();
    yield node;
    // reverse array, so left gets removed before right
    node.descendants.reverse().forEach(child => stack.add(child));
    }
    }

    Dacă aveți nevoie de o reîmprospătare a DFS, am acoperit-o în detaliu în postul Graph.

    Breadth-First Search (BFS)

    Similar cu DFS, putem implementa un BFS prin schimbarea Stack cu un Queue:

    BinarySearchTree.prototype.bfsFull Code
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    		 
    * bfs() {
    const queue = new Queue();
    queue.add(this.root);
    while (!queue.isEmpty()) {
    const node = queue.remove();
    yield node;
    node.descendants.forEach(child => queue.add(child));
    }
    }

    Ordinea BFS este: 

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11

    : 10, 5, 30, 4, 15, 40, 3

    Arbori echilibrați vs. arbori neechilibrați

    Până acum, am discutat despre cum să add, remove și find elemente. Cu toate acestea, nu am vorbit despre timpii de execuție. Să ne gândim la scenariile cele mai nefavorabile.

    Să spunem că vrem să adunăm numere în ordine crescătoare.

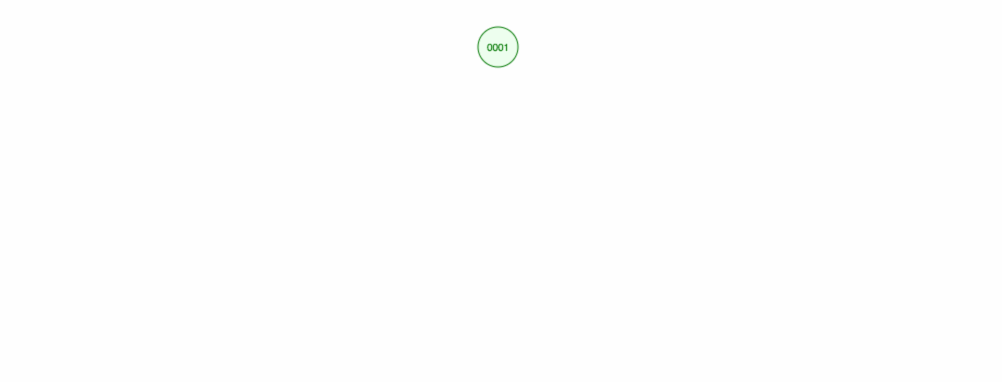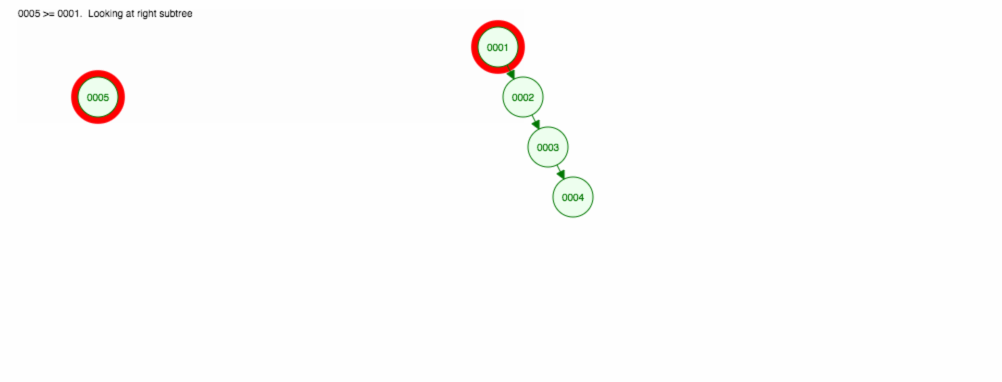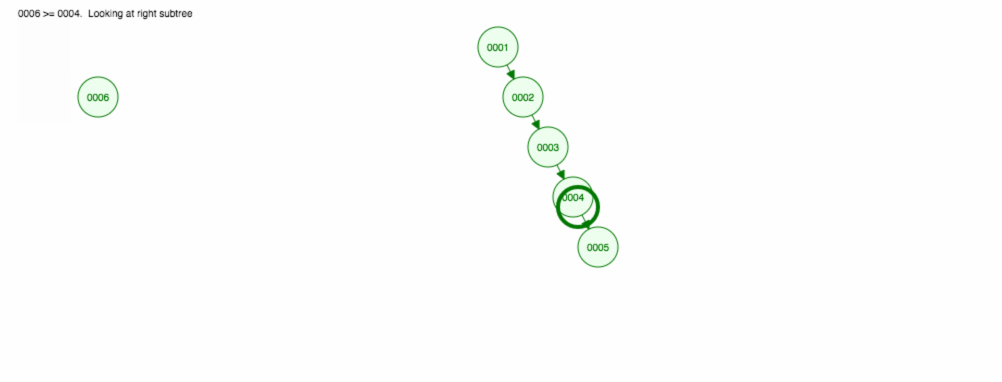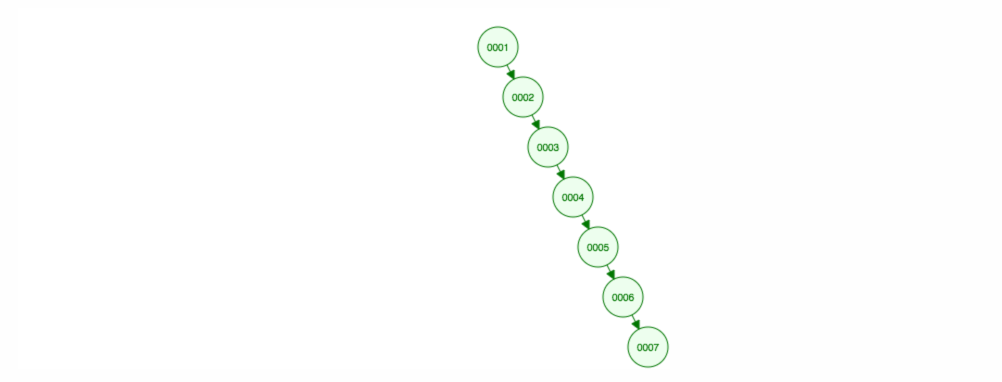
    Vom ajunge să avem toate nodurile în partea dreaptă! Acest arbore dezechilibrat nu este mai bun decât un LinkedList, astfel încât găsirea unui element ar dura O(n). 😱

    Căutarea a ceva într-un arbore dezechilibrat este ca și cum am căuta un cuvânt în dicționar pagină cu pagină. Când arborele este echilibrat, puteți deschide dicționarul la mijloc și, de acolo, știți dacă trebuie să mergeți la stânga sau la dreapta, în funcție de alfabet și de cuvântul pe care îl căutați.

    Trebuie să găsim o modalitate de a echilibra arborele!

    Dacă arborele ar fi echilibrat, am putea găsi elemente în O(log n) în loc să trecem prin fiecare nod. Să vorbim despre ce înseamnă un arbore echilibrat.

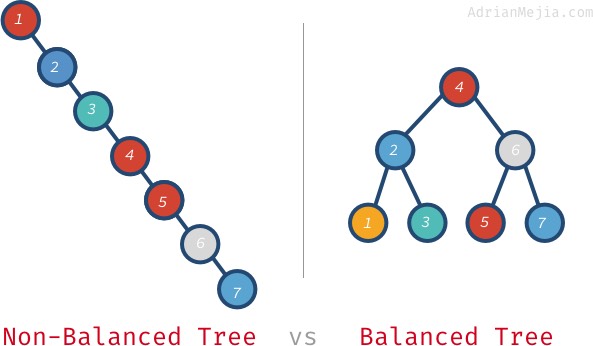
    Dacă căutăm 7 în arborele neechilibrat, trebuie să mergem de la 1 la 7. Totuși, în arborele echilibrat, vizităm: 4, 6, și 7. Situația se înrăutățește și mai mult cu arbori mai mari. Dacă aveți un milion de noduri, căutarea unui element inexistent ar putea necesita să vizitați toate milioanele, în timp ce pe un arbore echilibrat. Este nevoie doar de 20 de vizite! Este o diferență uriașă!

    Vom rezolva această problemă în următoarea postare folosind arbori auto-echilibrați (arbori AVL).

    Rezumat

    Am acoperit mult teren pentru arbori. Să rezumăm cu gloanțe:

    • Arborul este o structură de date în care un nod are 0 sau mai mulți descendenți/copii.
    • Nodurile arborilor nu au cicluri (aciclice). Dacă are cicluri, este în schimb o structură de date Graph.
    • Arborii cu doi copii sau mai puțin se numesc: Arbore binar
    • Când un arbore binar este sortat astfel încât valoarea din stânga să fie mai mică decât cea a părintelui și copiii din dreapta să fie mai mari, atunci și numai atunci avem un arbore de căutare binar.
    • Puteți vizita un arbore în mod pre/post/in-ordine.
    • Un arbore neechilibrat are o complexitate în timp de O(n). 🤦🏻
    • Un arbore echilibrat are o complexitate în timp de O(log n). 🎉

Lasă un răspuns

Adresa ta de email nu va fi publicată.