Träddatastrukturer har många användningsområden och det är bra att ha en grundläggande förståelse för hur de fungerar. Träd är grunden för andra mycket använda datastrukturer som kartor och uppsättningar. Dessutom används de på databaser för att utföra snabba sökningar. I HTML DOM används en träddatastruktur för att representera elementens hierarki. Det här inlägget kommer att utforska de olika typerna av träd som binära träd, binära sökträd och hur man implementerar dem.

Vi utforskade grafiska datastrukturer i det föregående inlägget, som är ett generaliserat fall av träd. Låt oss börja lära oss vad träddatastrukturer är!

Detta inlägg är en del av en handledningsserie:

Lär dig datastrukturer och algoritmer (DSA) för nybörjare

1. Intro till algoritmers tidskomplexitet och Big O-notation

2. Åtta tidskomplexiteter som varje programmerare bör känna till

3. Datastrukturer för nybörjare: Arrays, HashMaps och listor

4. Grafiska datastrukturer för nybörjare

5. Träd Datastrukturer för nybörjare 👈 du är här

6. Självbalanserade binära sökträd

7. Anhang I: Analys av rekursiva algoritmer

Träd: grundläggande begrepp

Ett träd är en datastruktur där en nod kan ha noll eller fler barn. Varje nod innehåller ett värde. Precis som i grafer kallas förbindelsen mellan noder för kanter. Ett träd är en typ av graf, men alla grafer är inte träd (mer om det senare).

Dessa datastrukturer kallas ”träd” eftersom datastrukturen liknar ett träd 🌳. Den börjar med en rotnod och förgrenar sig med dess underordnade och slutligen finns det blad.

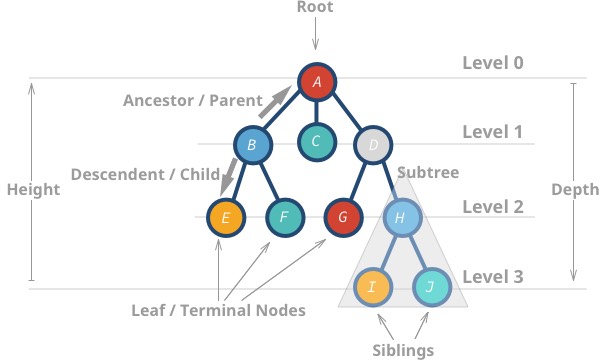
Här är några egenskaper hos träd:

• Den översta noden kallas rot.
• En nod utan barn kallas bladnod eller terminalnod.
• Trädens höjd (h) är avståndet (antalet kanter) mellan det längst bort belägna bladet och roten.
  • A A har en höjd på 3
  • I har en höjd på 0
• En nods djup eller nivå är avståndet mellan roten och noden i fråga.
  • H har ett djup på 2
  • B har ett djup på 1

Implementering av en enkel träddatastruktur

Som vi såg tidigare är en trädnod bara en datastruktur med ett värde och länkar till dess underordnade.

Här är ett exempel på en trädnod:

1
2
3
4
5
6

class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
}
}

Vi kan skapa ett träd med tre underordnade enligt följande:

1
2
3
4
5
6
7
8
9
10

// create nodes with values
const abe = new TreeNode('Abe');
const homer = new TreeNode('Homer');
const bart = new TreeNode('Bart');
const lisa = new TreeNode('Lisa');
const maggie = new TreeNode('Maggie');
// associate root with is descendants
abe.descendants.push(homer);
homer.descendants.push(bart, lisa, maggie);

Det var allt; vi har en träddatastruktur!

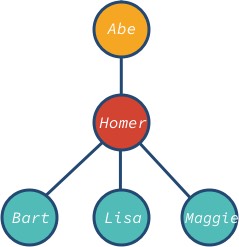
Noden abe är roten och bart, lisa och maggie är trädets bladnoder. Lägg märke till att trädets nod kan ha olika nedstigare: 0, 1, 3 eller något annat värde.

Träddatastrukturer har många användningsområden som:

• Kartor
• Mängder
• Databaser
• Prioritetsköer
• Frågning av en LDAP (Lightweight Directory Access Protocol)
• Representation av Document Object Model (DOM) för HTML på webbplatser.

Binära träd

Trädets noder kan ha noll eller flera barn. Men när ett träd har högst två barn kallas det binärt träd.

Fullständiga, fullständiga och perfekta binära träd

Avhängigt av hur noderna är ordnade i ett binärt träd kan det vara fullständigt, fullständigt och perfekt:

• Fullständigt binärt träd: varje nod har exakt 0 eller 2 barn (men aldrig 1).
• Fullständigt binärt träd: när alla nivåer utom den sista är fulla med noder.
• Perfekt binärt träd: när alla nivåer (inklusive den sista) är fulla med noder.

Se på dessa exempel:

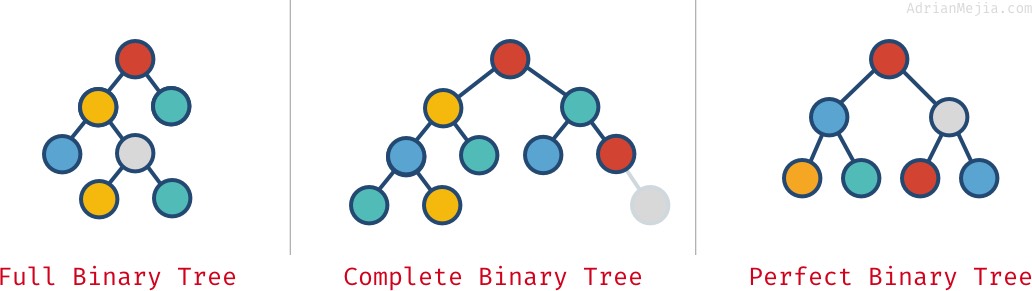
De här egenskaperna utesluter inte alltid varandra. Man kan ha fler än en:

• Ett perfekt träd är alltid komplett och fullt.
  • Perfekta binära träd har exakt `2^k – 1` noder, där k är trädets sista nivå (som börjar med 1).
• Ett komplett träd är inte alltid full.
  • Som i vårt ”kompletta” exempel, eftersom det har en förälder med bara ett barn. Om vi tar bort den grå noden längst till höger skulle vi ha ett komplett och fullständigt träd men inte perfekt.
• Ett fullständigt träd är inte alltid fullständigt och perfekt.

Binary Search Tree (BST)

Binary Search Trees eller kort och gott BST är en särskild tillämpning av binära träd. BST har högst två noder (som alla binära träd). Värdena är dock så att det vänstra barnvärdet måste vara mindre än föräldern och det högra barnvärdet måste vara högre.

Duplikat: Vissa BST tillåter inte dubbletter medan andra lägger till samma värden som ett högerbarn. Andra implementationer kan hålla en räkning på ett fall av duplicitet (vi kommer att göra detta senare).

Låt oss implementera ett binärt sökträd!

BST-implementation

BST är mycket lika vår tidigare implementering av ett träd. Det finns dock några skillnader:

• Noder kan högst ha två barn: vänster och höger.
• Nodernas värden måste vara ordnade som left < parent < right.

Här är trädets nod. Mycket lik det vi gjorde tidigare, men vi har lagt till några praktiska getters och setters för vänster och höger barn. Notera håller också en referens till föräldern, och vi uppdaterar den varje gång vi lägger till barn.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

const LEFT = 0;
const RIGHT = 1;
class TreeNode {
constructor(value) {
this.value = value;
this.descendants = ;
this.parent = null;
}
get left() {
return this.descendants;
}
set left(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
get right() {
return this.descendants;
}
set right(node) {
this.descendants = node;
if (node) {
node.parent = this;
}
}
}

Okej, än så länge kan vi lägga till ett vänster och höger barn. Nu ska vi göra BST-klassen som verkställer left < parent < right-regeln.

1
2
3
4
5
6
7
8
9
10
11
12
13

class BinarySearchTree {
constructor() {
this.root = null;
this.size = 0;
}
add(value) { /* ... */ }
find(value) { /* ... */ }
remove(value) { /* ... */ }
getMax() { /* ... */ }
getMin() { /* ... */ }
}

Låt oss implementera insättning.

BST Node Insertion

För att infoga en nod i ett binärt träd gör vi följande:

1. Om trädet är tomt blir den första noden roten och du är klar.
2. Genomför rot/föräldrars värde: om det är högre går du till höger, om det är lägre går du till vänster. Om det är samma värde finns värdet redan så att du kan öka antalet dubbletter (multiplicitet).
3. Upprepa #2 tills vi har hittat en tom plats för att infoga den nya noden.

Låt oss göra en illustration av hur man infogar 30, 40, 10, 15, 12, 50:

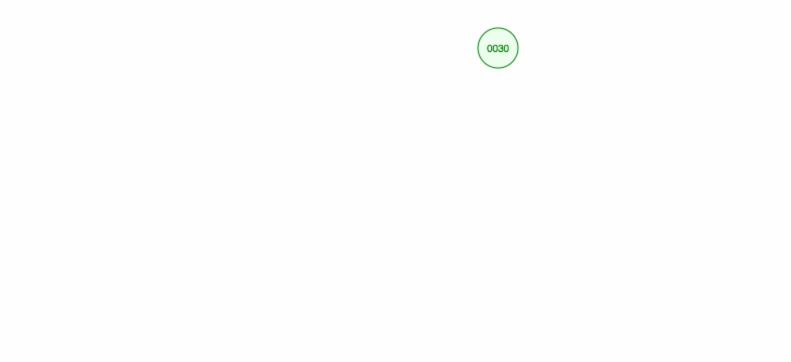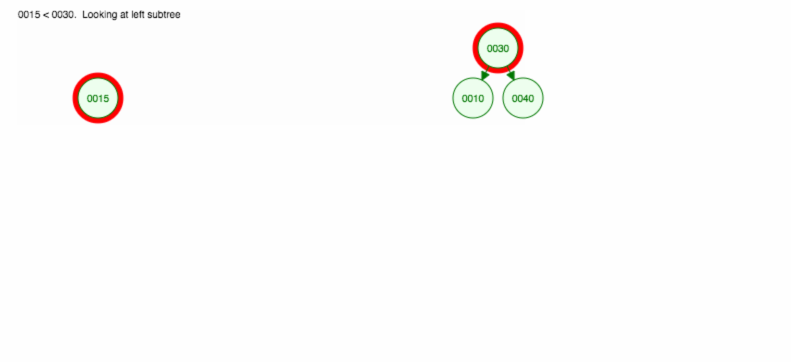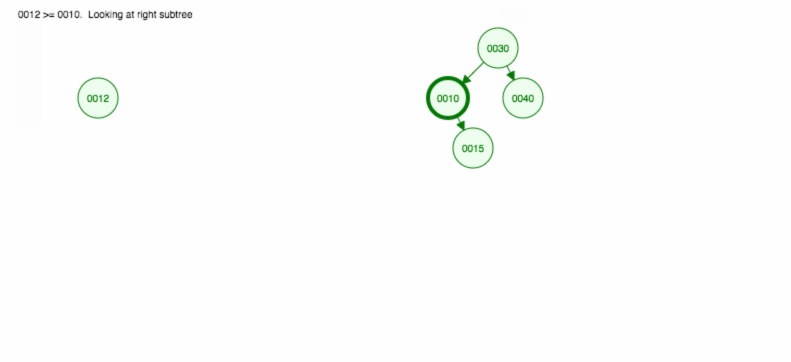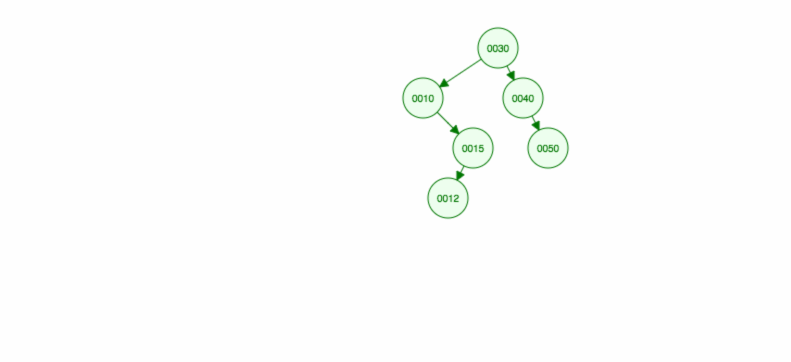
Vi kan implementera infoga på följande sätt:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

add(value) {
const newNode = new TreeNode(value);
if (this.root) {
const { found, parent } = this.findNodeAndParent(value);
if (found) { // duplicated: value already exist on the tree
found.meta.multiplicity = (found.meta.multiplicity || 1) + 1;
} else if (value < parent.value) {
parent.left = newNode;
} else {
parent.right = newNode;
}
} else {
this.root = newNode;
}
this.size += 1;
return newNode;
}

Vi använder en hjälpfunktion som heter findNodeAndParent. Om vi har funnit att noden redan finns i trädet ökar vi multiplicity-räknaren. Låt oss se hur den här funktionen implementeras:

1
2
3
4
5
6
7
8
9
10
11
12
13
14

findNodeAndParent(value) {
let node = this.root;
let parent;
while (node) {
if (node.value === value) {
break;
}
parent = node;
node = ( value >= node.value) ? node.right : node.left;
}
return { found: node, parent };
}

findNodeAndParent går igenom trädet och söker efter värdet. Den börjar vid roten (rad 2) och går sedan till vänster eller höger beroende på värdet (rad 10). Om värdet redan finns, returneras noden found och även den överordnade noden. Om noden inte finns återger vi fortfarande parent.

BST Node Deletion

Vi vet hur man infogar och söker efter värde. Nu ska vi implementera åtgärden radering. Det är lite knepigare än att lägga till, så vi förklarar det med följande fall:

Släcka en bladnod (0 barn)

1
2
3
4
5
6
7

 30 30
/ \ remove(12) / \
10 40 ---------> 10 40
\ / \ \ / \
15 35 50 15 35 50
/
12*

Vi tar bort referensen från nodens överordnade nod (15) för att den ska vara noll.

Släcka en nod med ett barn.

1
2
3
4
5

 30 30
/ \ remove(10) / \
10* 40 ---------> 15 40
\ / \ / \
15 35 50 35 50

I det här fallet går vi till föräldern (30) och ersätter barnet (10) med ett barns barn (15).

Raderar en nod med två barn

1
2
3
4
5

 30 30
/ \ remove(40) / \
15 40* ---------> 15 50
/ \ /
35 50 35

Vi tar bort nod 40, som har två barn (35 och 50). Vi ersätter förälderns (30) barn (40) med barnets högra barn (50). Sedan behåller vi det vänstra barnet (35) på samma plats som tidigare, så vi måste göra det till vänster barn till 50.

Ett annat sätt att ta bort nod 40 är att flytta det vänstra barnet (35) uppåt och sedan behålla det högra barnet (50) där det var.

1
2
3
4
5

 30
/ \
15 35
\
50

Det ena eller andra sättet är okej så länge du behåller egenskapen binärt sökträd: left < parent < right.

Radera roten.

1
2
3
4
5

 30* 50
/ \ remove(30) /
15 50 ---------> 35
/ /
35 15

Radera roten liknar i mångt och mycket det som tidigare diskuterades om att ta bort noder med 0, 1 eller 2 barn. Den enda skillnaden är att vi efteråt måste uppdatera referensen till trädets rot.

Här är en animation av det vi diskuterade.

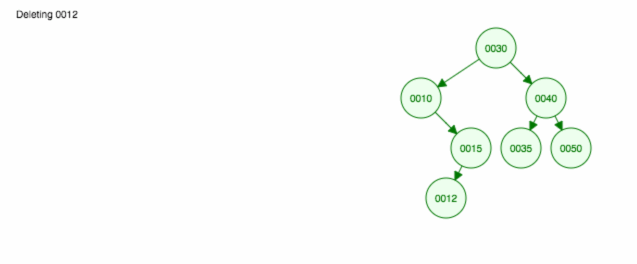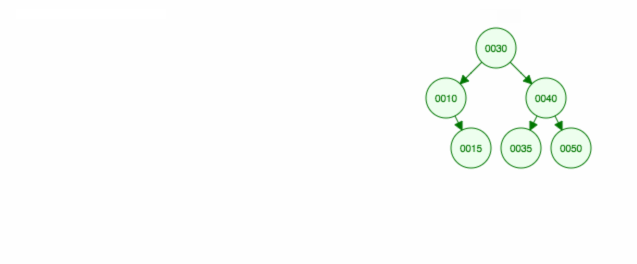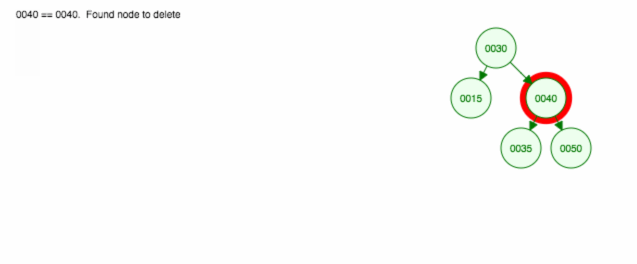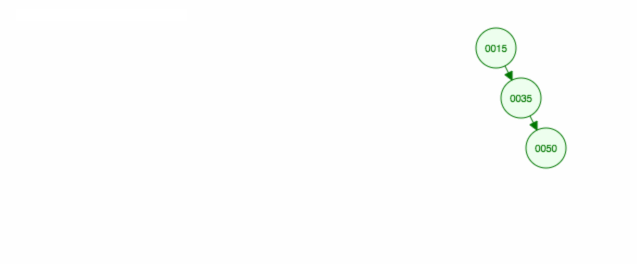
Animationen flyttar upp det vänstra barnet/delträdet och håller det högra barnet/delträdet på plats.

Nu när vi har en bra idé om hur det ska fungera, låt oss implementera det:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

remove(value) {
const nodeToRemove = this.find(value);
if (!nodeToRemove) return false;
// Combine left and right children into one subtree without nodeToRemove
const nodeToRemoveChildren = this.combineLeftIntoRightSubtree(nodeToRemove);
if (nodeToRemove.meta.multiplicity && nodeToRemove.meta.multiplicity > 1) {
nodeToRemove.meta.multiplicity -= 1; // handle duplicated
} else if (nodeToRemove === this.root) {
// Replace (root) node to delete with the combined subtree.
this.root = nodeToRemoveChildren;
this.root.parent = null; // clearing up old parent
} else {
const side = nodeToRemove.isParentLeftChild ? 'left' : 'right';
const { parent } = nodeToRemove; // get parent
// Replace node to delete with the combined subtree.
parent = nodeToRemoveChildren;
}
this.size -= 1;
return true;
}

Här är några höjdpunkter i implementationen:

• Först söker vi om noden finns. Om den inte gör det returnerar vi false, och vi är klara!
• Om noden som ska tas bort finns, kombinerar vi vänster och höger barn till ett delträd.
• Ersätt noden som ska tas bort med det kombinerade delträdet.

Funktionen som kombinerar vänster till höger delträd är följande:

1
2
3
4
5
6
7
8

combineLeftIntoRightSubtree(node) {
if (node.right) {
const leftmost = this.getLeftmost(node.right);
leftmost.left = node.left;
return node.right;
}
return node.left;
}

Till exempel, låt oss säga att vi vill kombinera följande träd och att vi är på väg att ta bort nod 30. Vi vill blanda 30:s vänstra delträd med det högra. Resultatet blir så här:

1
2
3
4
5
6
7

 30* 40
/ \ / \
10 40 combine(30) 35 50
\ / \ -----------> /
15 35 50 10
\
15

Om vi gör det nya underträdet till roten, så finns nod 30 inte längre!

Binary Tree Transversal

Det finns olika sätt att traversera ett binärt träd, beroende på i vilken ordning noderna besöks: in-order, pre-order och post-order. Vi kan också använda demDFSochBFSsom vi lärde oss från grafen post.Låt oss gå igenom var och en av dem.

In-order Traversal

In-order traversal besöker noder i denna ordning: vänster, förälder, höger.

1
2
3
4
5

* inOrderTraversal(node = this.root) {
if (node.left) { yield* this.inOrderTraversal(node.left); }
yield node;
if (node.right) { yield* this.inOrderTraversal(node.right); }
}

Låt oss använda detta träd för att göra exemplet:

1
2
3
4
5
6
7

 10
/ \
5 30
/ / \
4 15 40
/
3

En genomgång i rätt ordning skulle ge följande värden: 3, 4, 5, 10, 15, 30, 40. Om trädet är ett BST kommer noderna att sorteras i stigande ordning som i vårt exempel.

Post-Order Traversal

Post-Order traversal besöker noderna i denna ordning: vänster, höger, parent.

1
2
3
4
5

* postOrderTraversal(node = this.root) {
if (node.left) { yield* this.postOrderTraversal(node.left); }
if (node.right) { yield* this.postOrderTraversal(node.right); }
yield node;
}

Post-order traversal skulle skriva ut följande värden: 3, 4, 5, 15, 40, 30, 10.

Pre-order Traversal and DFS

Pre-order traversal visit nodes on this order: parent, left, right.

1
2
3
4
5

* preOrderTraversal(node = this.root) {
yield node;
if (node.left) { yield* this.preOrderTraversal(node.left); }
if (node.right) { yield* this.preOrderTraversal(node.right); }
}

Pre-order traversal skulle skriva ut följande värden: 10, 5, 4, 3, 30, 15, 40. Denna ordning av siffror är samma resultat som vi skulle få om vi kör DFS (Depth-First Search).

1
2
3
4
5
6
7
8
9
10
11
12

* dfs() {
const stack = new Stack();
stack.add(this.root);
while (!stack.isEmpty()) {
const node = stack.remove();
yield node;
// reverse array, so left gets removed before right
node.descendants.reverse().forEach(child => stack.add(child));
}
}

Om du behöver en uppfräschning av DFS, har vi behandlat det i detalj i Graph post.

Breadth-First Search (BFS)

Som liknar DFS kan vi implementera en BFS genom att byta ut Stack mot en Queue:

1
2
3
4
5
6
7
8
9
10
11

* bfs() {
const queue = new Queue();
queue.add(this.root);
while (!queue.isEmpty()) {
const node = queue.remove();
yield node;
node.descendants.forEach(child => queue.add(child));
}
}

BFS ordningen är: 10, 5, 30, 4, 15, 40, 3

Balanserade vs. icke-balanserade träd

Sedan tidigare har vi diskuterat hur vi ska add, remove och find element. Vi har dock inte talat om körtider. Låt oss tänka på de värsta scenarierna.

Då vi säger att vi vill addera siffror i stigande ordning.

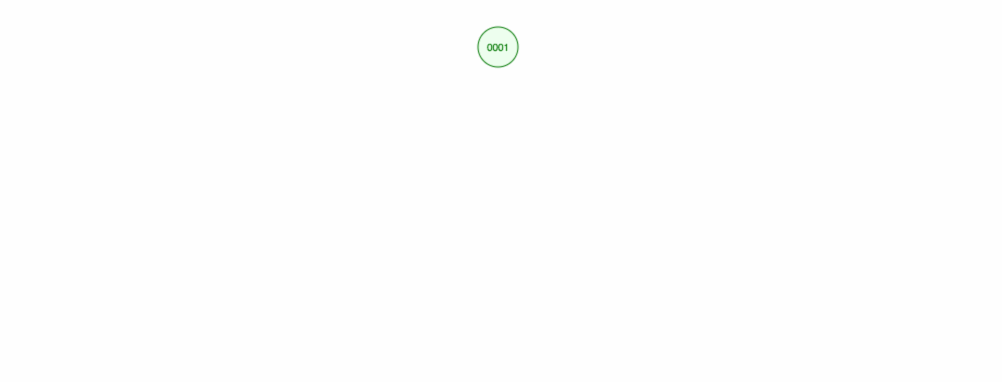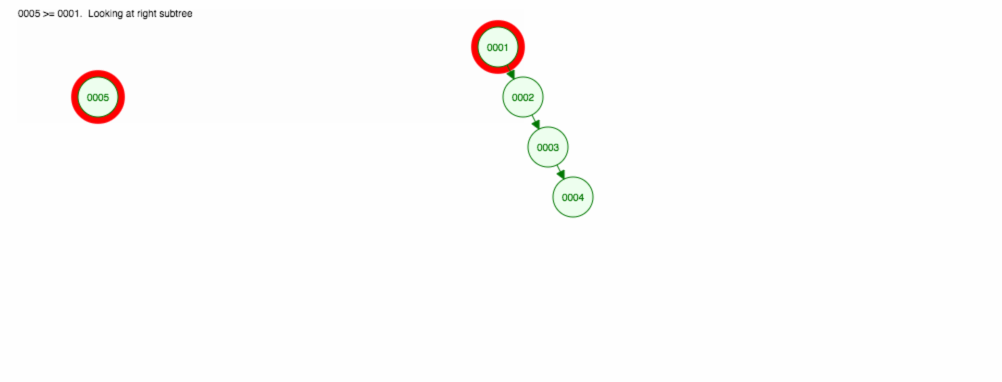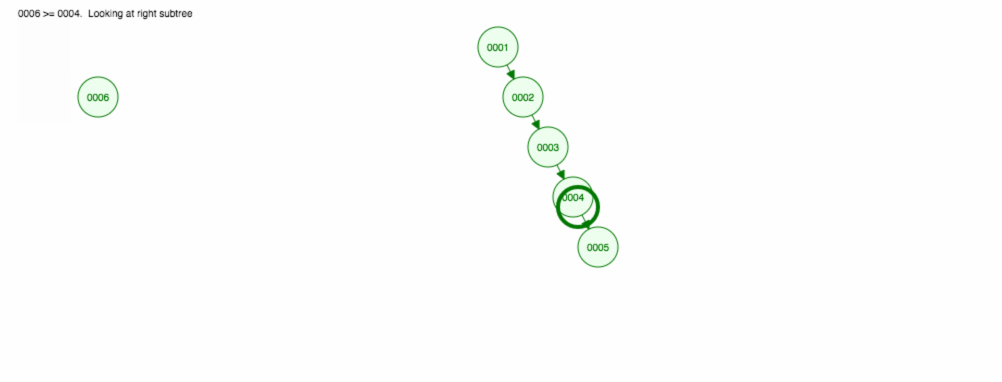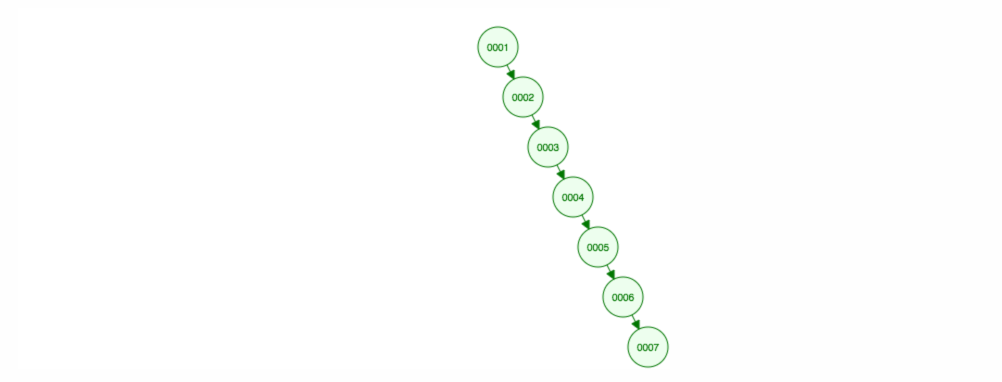
Vi kommer att hamna med alla noder på den högra sidan! Detta obalanserade träd är inte bättre än en LinkedList, så att hitta ett element skulle ta O(n). 😱

Att leta efter något i ett obalanserat träd är som att leta efter ett ord i ordboken sida för sida. När trädet är balanserat kan du öppna ordboken i mitten, och därifrån vet du om du måste gå till vänster eller höger beroende på alfabetet och det ord du letar efter.

Vi måste hitta ett sätt att balansera trädet!

Om trädet var balanserat skulle vi kunna hitta element på O(log n) istället för att gå igenom varje nod. Låt oss tala om vad ett balanserat träd innebär.

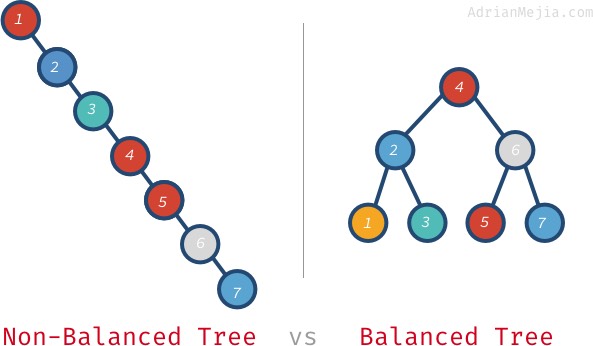
Om vi söker efter 7 i det icke balanserade trädet måste vi gå från 1 till 7. Men i det balanserade trädet besöker vi: 4, 6 och 7. Det blir ännu värre med större träd. Om du har en miljon noder kan sökandet efter ett icke-existerande element kräva att du besöker alla miljoner medan du i ett balanserat träd. Det behövs bara 20 besök! Det är en enorm skillnad!

Vi kommer att lösa detta problem i nästa inlägg med hjälp av självbalanserade träd (AVL-träd).

Sammanfattning

Vi har täckt mycket mark för träd. Låt oss sammanfatta det med punkter:

• Trädet är en datastruktur där en nod har 0 eller fler efterkommande/barn.
• Trädets noder har inga cykler (acykliska). Om den har cykler är det istället en Graph-datastruktur.
• Träd med två barn eller färre kallas: Binärt träd
• När ett binärt träd sorteras så att det vänstra värdet är mindre än föräldern och de högra barnen är högre, då och endast då har vi ett binärt sökträd.
• Du kan besöka ett träd på ett för/efter/in-ordningsmässigt sätt.
• En obalanserad har en tidskomplexitet på O(n). 🤦🏻
• En balanserad har en tidskomplexitet på O(log n). 🎉