Fysikalisk kemi är ett ganska brett ämne; det omfattar:

• Kvantkemi
• Thermokemi (genomgång + mer)
• Kinetik (genomgång + mer)
• Statistisk mekanik

Då det finns ganska många ämnen för ett svar, kommer jag bara att ge två exempel per ämne. Detta kommer att bli ett långt svar, men du kan fokusera på det du söker.

KVALANTKEMI

Kvantkemi handlar i allmänhet om att försöka förstå scenarier på picoskopisk skala, att modellera system i bekväma matematiska representationer och att göra lämpliga approximationer.

Två exempel på kvantkemi är:

• Enkel harmonisk oscillator (två bollar förbundna med en idealfjäder)

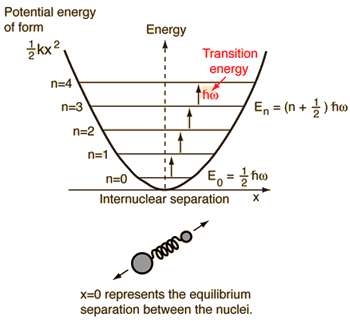
För detta system, som vi känner till från fysiken, reducerar vi det från ett klassiskt tvåkroppsproblem till ett enkroppsproblem med relativa koordinater och en reducerad massa, #mu = (m_1m_2)/(m_1 + m_2)#.

Detta system är inriktat på att förstå den elastiska potentiella energin hos molekylbindningen.

• Styv rotor (två bollar förbundna med en stång, dvs. 100 % styv fjäder)

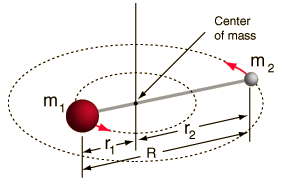
Detta system är en förenkling, eftersom alla molekyler har någon form av bindningssträckning/vibration (du skulle förstå varför denna förenkling är okej, om du såg matematiken!).

Det gör det dock möjligt för oss att dekomponera denna vinkelkomponent av ett tvåkroppssystem och förstå molekylens rotationsegenskaper.

THERMOKEMI

Detta tittar på den makroskopiska skalan för värmeflöde, arbete, fria energier och så vidare. Du har gjort detta tidigare i allmän kemi något, och detta gås igenom och utökas.

Två exempel är:

• Bestämning av termodynamiska värden från mätbara storheter

Vad är kemi om den inte är praktisk?

Så ett gemensamt tema är att kunna utföra härledningar och uttrycka de viktigaste termodynamiska storheterna (entropi, entalpi, Gibbs + Helmholtz fria energi, inre energi) i termer av naturliga variabler som volym, temperatur och tryck.

Man kan till exempel beräkna entropin från en isotermisk expansion (#DeltaT = 0, DeltaV > 0#) genom att känna till #V_2# och #V_1#, eller #P_2# och #P_1#, och detta för en monatomär idealgas:

##DeltaS = -nRln(P_2/P_1) = nRln(V_2/V_1)#

• Ideal and Non-Ideal Non-Electrolyte/Electrolyte Solutions

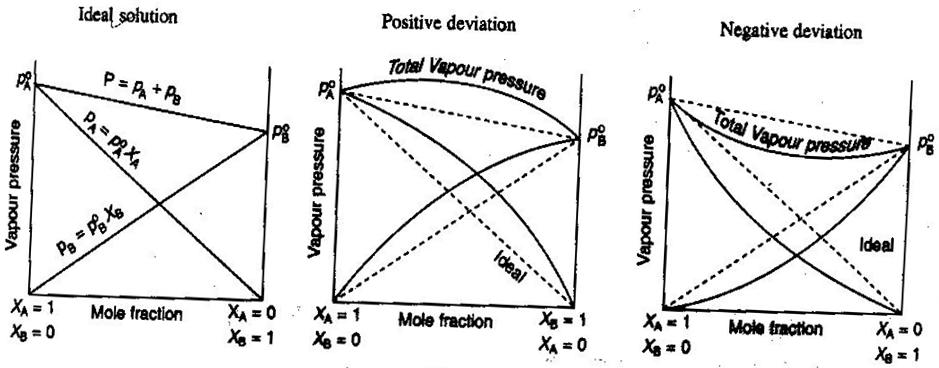
I allmän kemi, vill vi behandla lösningar idealiskt, så att volymer är additiva, koncentrationer av starka elektrolyter är raka #”mol/L ”#beräkningar och så vidare. Några sätt på vilka lösningar kanske inte är idealiska:

• Lösningen kan expandera eller krympa efter att ha blandats.
• Ionparning minskar lösningens jonstyrka och minskar van’t Hoff-faktorn #i# för den lösta substansen.
• Den lösta ämnets flyktbenägenhet ändrar dess effektiva koncentration (dess aktivitet).

KINETIK

Du kanske har gjort det här tidigare i en allmän kemikurs, eller kanske i gymnasiet. Fysikalisk kemi utökar detta lite mer genom att titta närmare på reaktionsmekanismer och gasfasdynamik.

Två exempel:

• Steady-State-approximation

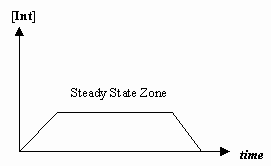
Ibland är hastigheten för det första mekanistiska steget mycket långsammare än hastigheten för det andra steget, och vi approximerar att koncentrationen av intermediären i praktiken inte förändras (#(d)/(dt) = 0#).

Detta gör det möjligt att härleda en hastighetslag som är specifik för en mekanism, och för oss att uttrycka en ”observerad hastighetskonstant” i termer av hastighetskonstanter för de enskilda stegen.

• Realgaslagar

Du kanske har blivit introducerad till van der Waals tillståndsekvation:

#(V – nb) = nRT#

Nja, det finns några andra, som Redlich-Kwong, Peng-Robinson, och så vidare.

Den grundläggande idén är att de alla fungerar bättre för vissa gaser än andra, men de fungerar alla för att ta hänsyn till gasernas verkliga egenskaper i stället för att anta att alla är en elastiskt kolliderande inert punktmassa.

STATISTISK MEKANIK

Med statistisk mekanik tar vi ett steg tillbaka och betraktar den picoskopiska världen ur ett makroskopiskt perspektiv:

”Vad kan vi lära oss om ett system om vi tänker som en kvantkemist på en stor samling partiklar?”

Två exempel:

• Equipartitionssats

#<< K >> = N/2nRT = N/2 k_BT#,

där #N# är antalet frihetsgrader för varje typ av rörelse (linjär, rotations-, vibrations-, elektron- och kärnrörelse). I princip tar man hänsyn till varje typ av rörelse i en molekyl för att uppskatta dess genomsnittliga kinetiska energi, #<< K >>#.

Detta fungerar endast vid ”tillräckligt höga” temperaturer. Vanligtvis är det OK för translations- och rotationsrörelser, men det tenderar att överskatta vibrationsbidrag.

• Den mikrokanoniska partitionsfunktionen

#q = sum_(i=1)^(N) g_ie^(-beta epsilon_i)#,

här:

• #g_i# är degenerationen av tillståndet #i# med energi #epsilon_i#.
• #N# är det totala antalet tillgängliga tillstånd.

På samma sätt som vågfunktionen #psi# specificerar allt som finns att veta om ett kvantmekaniskt system, specificerar den mikrokanoniska fördelningsfunktionen hur en molekyl kan fördela sin tillgängliga energi på de möjliga typerna av tillstånd (translations-, rotations-, vibrations-, elektroniska och nukleära tillstånd).

Det finns en #q# för varje typ av tillstånd: Det finns en #q_(tr)#, #q_(rot)#, #q_(vib)#, #q_(el ec)# och #q_(n uc)#.

Från kunskapen om varje typ av #q# kan de välkända termodynamiska storheterna härledas, t.ex. entropi (#S#), entalpi (#H#), Gibbs fria energi (#G#), osv. i termer av varje typ av #q#.

Som ett användbart exempel kan den absoluta molekylära entropin vid ALLA temperaturer i de flesta fall beräknas som:

#S/N = k_B ln (q/N)_”tot” + (<< epsilon >>_”tot”)/T + k_B#,

varvid:

• #k_B ~~ ”0.695 cm”^(-1)”/K ”# är Boltzmannkonstanten.
• #(q/N)_”tot” = (q_(tr))/Nq_(rot)q_(vib)q_(el ec)q_(n uc)# är den totala mikrokanoniska fördelningsfunktionen som innefattar alla möjliga typer av tillstånd, och #N# är det totala antalet molekyler som beaktas.
• #

(Ja, med denna formel vid #”298,15 K ”# kan du beräkna samma #S^@# som du ser i din läroboksbilaga!)

Ett exempel på hur denna formel används finns här.